题目内容
10.(1)解不等式组$\left\{\begin{array}{l}{3x+3>0}\\{2(x+5)≥6(x-1)}\end{array}\right.$(2)在(1)的条件下化简:|x+1|+|x-4|
分析 (1)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集;
(2)根据绝对值的性质去绝对值符号,再合并即可得.
解答 解:(1)解不等式3x+3>0,得:x>-1,
解不等式2(x+5)≥6(x-1),得:x<4,
则不等式组的解集为-1<x<4;
(2)原式=x+1-(x-4)
=x+1-x+4
=5.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20. 若三个正方形的面积如图所示,则正方形A的面积为( )
若三个正方形的面积如图所示,则正方形A的面积为( )
 若三个正方形的面积如图所示,则正方形A的面积为( )
若三个正方形的面积如图所示,则正方形A的面积为( )| A. | 6 | B. | 36 | C. | 64 | D. | 8 |
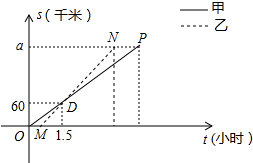 顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1(h)到达B地,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,a表示A、B两地之间的距离.请结合图中的信息解决如下问题:
顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1(h)到达B地,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,a表示A、B两地之间的距离.请结合图中的信息解决如下问题:
 已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,沿AC方向,以每秒1个单位的速度向终点C运动,设点P运动时间为t秒.
已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,沿AC方向,以每秒1个单位的速度向终点C运动,设点P运动时间为t秒.