Question

11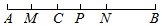．如图，点C是线段AB上一点，点M，N，P分别是线段AC，BC，AB的中点．
（1）若AB=12cm，则MN的长度是6cm；
（2）若AC=3cm，CP=1cm，求线段PN的长度．

Answer 1

分析 （1）利用线段中点的定义得到MC=$\frac{1}{2}$AC，CN=$\frac{1}{2}$BC，则MN=MC+CN=$\frac{1}{2}$AB=6cm；
（2）由已知条件可以求得AP=AC+CP=4cm，因为P是AB的中点，所以AB=2AP=8cm，BC=AB-AC=5cm，根据N为BC的中点，可求得CN=$\frac{1}{2}$BC=2.5cm，所以PN=CN-CP=1.5cm．

解答 解：（1）∵M、N分别是AC、BC的中点，
∴MC=$\frac{1}{2}$AC，CN=$\frac{1}{2}$BC，
∴MN=MC+CN=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$（AC+BC）=$\frac{1}{2}$AB=6cm．
故答案为6cm；

（2）∵AC=3cm，CP=1cm，
∴AP=AC+CP=4cm，
∵P是线段AB的中点，
∴AB=2AP=8cm．
∴CB=AB-AC=5cm，
∵N是线段CB的中点，CN=$\frac{1}{2}$CB=2.5cm，
∴PN=CN-CP=1.5cm．

点评 本题主要考查两点间的距离，线段的计算，正确理解线段中点的定义是解题的关键．