题目内容
17.已知∠AOB=45°,点P在∠AOB内部,点P1与点P关于OA对称,点P2与点P关于OB对称,则△P1OP2是( )| A. | 含30°角的直角三角形 | B. | 等腰直角三角形 | ||
| C. | 等边三角形 | D. | 顶角是30°的等腰三角形 |
分析 由P,P1关于直线OA对称,P、P2关于直线OB对称,推出OP=OP1=OP2,∠AOP=∠AOP1,∠BOP=∠BOP2,推出∠P1OP2=90°,由此即可判断.
解答 解:如图,
∵P,P1关于直线OA对称,P、P2关于直线OB对称,
∴OP=OP1=OP2,∠AOP=∠AOP1,∠BOP=∠BOP2,
∵∠AOB=45°,
∴∠P1OP2=2∠AOP+2∠BOP=2(∠AOP+∠BOP)=90°,
∴△P1OP2是等腰直角三角形.
故选B.
点评 本题考查轴对称的性质、等腰直角三角形的判定等知识,解题的关键是灵活运用对称的性质解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下列各式:-$\frac{1}{2}$mn,m,8,$\frac{1}{a}$,x2+2x+6,$\frac{2x-y}{5}$,$\frac{x^2+4y}{π}$,y3-5y+$\frac{1}{y}$中,整式有( )
| A. | 3个 | B. | 4个 | C. | 6个 | D. | 7个 |
2.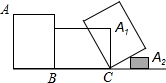 如图,长方形木板的长为4cm,宽为3cm,某同学使之在桌面上做无滑动的翻滚(顺时针方向),木板上点A的位置变化为A→Al→A2,其中第二次翻滚被桌面上的一块小木板挡住,使木板与桌面成30°,则点A滚到A2位置时走过的路径总长为( )
如图,长方形木板的长为4cm,宽为3cm,某同学使之在桌面上做无滑动的翻滚(顺时针方向),木板上点A的位置变化为A→Al→A2,其中第二次翻滚被桌面上的一块小木板挡住,使木板与桌面成30°,则点A滚到A2位置时走过的路径总长为( )
 如图,长方形木板的长为4cm,宽为3cm,某同学使之在桌面上做无滑动的翻滚(顺时针方向),木板上点A的位置变化为A→Al→A2,其中第二次翻滚被桌面上的一块小木板挡住,使木板与桌面成30°,则点A滚到A2位置时走过的路径总长为( )
如图,长方形木板的长为4cm,宽为3cm,某同学使之在桌面上做无滑动的翻滚(顺时针方向),木板上点A的位置变化为A→Al→A2,其中第二次翻滚被桌面上的一块小木板挡住,使木板与桌面成30°,则点A滚到A2位置时走过的路径总长为( )| A. | 10cm | B. | 3.5π cm | C. | 4.5π cm | D. | 2.5π cm |
6.下列说法正确的是( )
| A. | -a一定是负数 | B. | 两个数的和一定大于每一个加数 | ||
| C. | 若|m|=2,则m=±2 | D. | 若a+b=0,则a=b=0 |
7.若(x-1)2-1=0,则x的值为( )
| A. | ±1 | B. | ±2 | C. | -2或0 | D. | 0或2 |