题目内容
19. 如图,直线MN交⊙O于A、B两点,AC是⊙O的直径,AD平分∠CAM交⊙O于D,过点D作⊙O的切线交MN于点E.
如图,直线MN交⊙O于A、B两点,AC是⊙O的直径,AD平分∠CAM交⊙O于D,过点D作⊙O的切线交MN于点E.(1)求证:DE⊥MN;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
分析 (1)连接OD,由DE与⊙O相切知∠ODE=90°,由AD平分∠CAM及OD=OA知∠1=∠2=∠3,得OD∥MN,继而知DE⊥MN;
(2)连接DC,由勾股定理得AD=$\sqrt{D{E}^{2}+A{E}^{2}}$=3$\sqrt{5}$,证△DAE∽△CAD得$\frac{AE}{AD}$=$\frac{AD}{AC}$,即可知AC=$\frac{A{D}^{2}}{AE}$=15,从而得出答案.
解答 解:(1)如图,连接OD,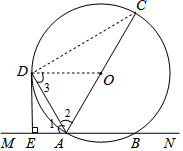
∵DE与⊙O相切于点D,
∴∠ODE=90°,
∵OD=OA,
∴∠2=∠3,
又∵∠1=∠2,
∴∠1=∠3,
∴OD∥MN,
∴DE⊥MN;
(2)连接DC,
∵AC是⊙O的切线,
∴∠ADC=90°,
又∵∠DEA=90°,∠1=∠2,
∴△DAE∽△CAD,
∴$\frac{AE}{AD}$=$\frac{AD}{AC}$,
又AD=$\sqrt{D{E}^{2}+A{E}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
∴AC=$\frac{A{D}^{2}}{AE}$=$\frac{(3\sqrt{5})^{2}}{3}$=15,
∴⊙O的半径OA=$\frac{15}{2}$.
点评 本题主要考查切线的性质、相似三角形的判定与性质,熟练掌握切线的性质及相似三角形的判定与性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.有一组数据:7,7,7,8,11,11,12,下列说法错误的是( )
| A. | 众数是7 | B. | 极差是5 | C. | 中位数是7 | D. | 平均数是9 |
7.下列各数中最小的数据是( )
| A. | -1 | B. | -$\sqrt{2}$ | C. | 0 | D. | 1 |
14.$\frac{\sqrt{2}}{2}$的倒数是( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{1}{2}$ |
8.PM2.5“超细灰尘”主要来自机动车尾气尘、燃油尘、硫酸盐、餐饮油烟尘、建筑水泥尘、煤烟尘和硝酸盐等,它是雾霾有害细颗粒的重要组成部分.而PM2.5可直接被人体吸入肺部,由于其穿透力强,因此对人类的危害非常大,PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )
| A. | 0.25×10-5 | B. | 0.25×10-6 | C. | 2.5×10-5 | D. | 2.5×10-6 |
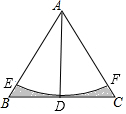 如图,△ABC是边长4的等边三角形,AD平分∠BAC交BC于D点.以A点为圆心,AD的长为半径画弧交分别边AB,AC于E,F两点,求图中阴影部分的面积4$\sqrt{3}$-2π.
如图,△ABC是边长4的等边三角形,AD平分∠BAC交BC于D点.以A点为圆心,AD的长为半径画弧交分别边AB,AC于E,F两点,求图中阴影部分的面积4$\sqrt{3}$-2π.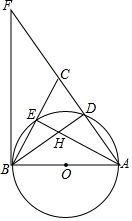 如图,在△ABC中,AB=AC,以AB为直径作⊙O分别交AC、BC于D、E,延长AC至F,连结BF,若∠CAB=2∠FBC.
如图,在△ABC中,AB=AC,以AB为直径作⊙O分别交AC、BC于D、E,延长AC至F,连结BF,若∠CAB=2∠FBC.