��Ŀ����
7�� ��ͼ����P1��x1��y1������P2��x2��y2����������Pn��xn��yn���ں���$y=\frac{1}{x}$��x��0����ͼ���ϣ���P1OA1����P2A1A2����P3A2A3��������PnAn-1An���ǵ���ֱ�������Σ�б��OA1��A1A2��A2A3������An-1An����x���ϣ�n�Ǵ��ڻ����2����������������P1OA2���ڽ�������B1C1D1E2���ܳ���Ϊl1����P2A1A2���ڽ�������B2C2D2E2���ܳ���Ϊl2��������PnAn-1An���ڽ�������BnCnDnEn���ܳ���Ϊln�����ú�n��ʽ�ӱ�ʾl1+l2+l3+��+lnΪ��������
��ͼ����P1��x1��y1������P2��x2��y2����������Pn��xn��yn���ں���$y=\frac{1}{x}$��x��0����ͼ���ϣ���P1OA1����P2A1A2����P3A2A3��������PnAn-1An���ǵ���ֱ�������Σ�б��OA1��A1A2��A2A3������An-1An����x���ϣ�n�Ǵ��ڻ����2����������������P1OA2���ڽ�������B1C1D1E2���ܳ���Ϊl1����P2A1A2���ڽ�������B2C2D2E2���ܳ���Ϊl2��������PnAn-1An���ڽ�������BnCnDnEn���ܳ���Ϊln�����ú�n��ʽ�ӱ�ʾl1+l2+l3+��+lnΪ��������| A�� | $\frac{8\sqrt{n}}{3}$ | B�� | 2$\sqrt{n}$ | C�� | $\frac{4\sqrt{n}}{3}$ | D�� | $\frac{2\sqrt{n}}{3}$ |
���� ���ڡ�P1OA1�ǵ���ֱ�������Σ���ֱ֪��OP1�Ľ���ʽΪy=x��������y=$\frac{1}{x}$��x��0�����������������Ľ⣬�õ���P1�����꣬��A1�ĺ�������P1�ĺ�������������Ӷ�ȷ����A1�����ꣻ���ڡ�P1OA1����P2A1A2���ǵ���ֱ�������Σ���A1P2��OP1��ֱ��A1P2�ɿ�����ֱ��OP1����ƽ��OA1����λ���ȵõ��ģ�����õ�ֱ��A1P2�Ľ���ʽ��ͬ����������y=$\frac{1}{x}$��x��0�����������������Ľ⣬�õ���P2�����꣬��P2�ĺ��������߶�A1A2���е㣬�Ӷ�ȷ����A2�����ꣻ�������ƣ��Ӷ�ȷ����An�����꣬�ó�OAn�ij���Ȼ�����l1=$\frac{4}{3}$OA1��l2=$\frac{4}{3}$A1A2��l3=$\frac{4}{3}$A2A3��ln=$\frac{4}{3}$An-1An���������l1+l2+l3+��+ln=$\frac{4}{3}$OAn=$\frac{4}{3}$��2 $\sqrt{n}$=$\frac{8}{3}$$\sqrt{n}$��
��� �⣺��P1��P1M1��x����M1����ͼ����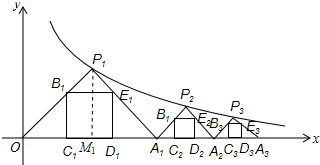
��֪M1��1��0����OA1���е㣬
��A1��2��0����
�ɵ�P1������Ϊ��1��1����
��P1O�Ľ���ʽΪ��y=x��
��P1O��A1P2��
��A1P2�ı���ʽһ����ϵ����ȣ�
��A1��2��0������y=x+b��
��b=-2��
��A1P2�ı���ʽ��y=x-2��
��y=$\frac{1}{x}$��x��0�����������P2��1+$\sqrt{2}$��-1+$\sqrt{2}$����
���ϣ�A2��2$\sqrt{2}$��0����
P3��$\sqrt{2}$+$\sqrt{3}$��-$\sqrt{2}$+$\sqrt{3}$����A3��2$\sqrt{3}$��0����
�������ƣ���An������Ϊ��2$\sqrt{n}$��0����
��l1=$\frac{4}{3}$OA1��l2=$\frac{4}{3}$A1A2��l3=$\frac{4}{3}$A2A3��ln=$\frac{4}{3}$An-1An��
��l1+l2+l3+��+ln=$\frac{4}{3}$OAn=$\frac{4}{3}$��2$\sqrt{n}$=$\frac{8}{3}$$\sqrt{n}$��
��ѡ��A��
���� ���⿼���˷���������ͼ���ϵ����������������ֱ�������ε����ʣ������ε����ʵȣ��ؼ����ҳ���P������Ĺ��ɣ����������Ϊ�������Pn�ĺ����꣬�������An�ĺ������ֵ���Ӷ��ɵó�����Ľ����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | ���� | B�� | ���� | C�� | ƽ���� | D�� | ��λ�� |
| A�� | $\sqrt{18}$ | B�� | $\sqrt{\frac{1}{3}}$ | C�� | $\sqrt{24}$ | D�� | $\sqrt{0.3}$ |
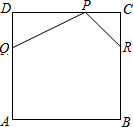 ��ͼ��������ABCD��һ�ű߳�Ϊ12���ֵ�Ƥ�Ƥ��ʦ�����ڴ�Ƥ�������ڵĽ���ֱ����¡�PDQ���PCR��õ�һ�������PQABR������PD=2DQ��PC=RC����P��Q��
��ͼ��������ABCD��һ�ű߳�Ϊ12���ֵ�Ƥ�Ƥ��ʦ�����ڴ�Ƥ�������ڵĽ���ֱ����¡�PDQ���PCR��õ�һ�������PQABR������PD=2DQ��PC=RC����P��Q��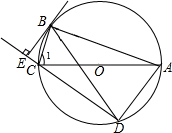 ��ͼ����O�ǡ�ABC�����Բ��ACΪֱ������BD=BA��BE��DC��DC���ӳ����ڵ�E��
��ͼ����O�ǡ�ABC�����Բ��ACΪֱ������BD=BA��BE��DC��DC���ӳ����ڵ�E�� ��ͼ��AB��CD��AE��CD�ڵ�C��DE��AE�ڵ�E������A=42�㣬���D=48�㣮
��ͼ��AB��CD��AE��CD�ڵ�C��DE��AE�ڵ�E������A=42�㣬���D=48�㣮