题目内容
12. 如图,AB∥CD,AE交CD于点C,DE⊥AE于点E,若∠A=42°,则∠D=48°.
如图,AB∥CD,AE交CD于点C,DE⊥AE于点E,若∠A=42°,则∠D=48°.
分析 首先根据平行线的性质求得∠ECD的度数,然后在直角△ECD中,利用三角形内角和定理求解.
解答 解:∵AB∥CD,
∴∠ECD=∠A=42°,
又∵DE⊥AE,
∴直角△ECD中,∠D=90°-∠ECD=90°-42°=48°.
故答案为:48°.
点评 本题考查了平行线的性质以及三角形内角和定理,正确理解定理是关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
3.下列图形中,属于立体图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7. 如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),若△P1OA2的内接正方形B1C1D1E2的周长记为l1,△P2A1A2的内接正方形B2C2D2E2的周长记为l2,…,△PnAn-1An的内接正方形BnCnDnEn的周长记为ln,则用含n的式子表示l1+l2+l3+…+ln为( )
如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),若△P1OA2的内接正方形B1C1D1E2的周长记为l1,△P2A1A2的内接正方形B2C2D2E2的周长记为l2,…,△PnAn-1An的内接正方形BnCnDnEn的周长记为ln,则用含n的式子表示l1+l2+l3+…+ln为( )
 如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),若△P1OA2的内接正方形B1C1D1E2的周长记为l1,△P2A1A2的内接正方形B2C2D2E2的周长记为l2,…,△PnAn-1An的内接正方形BnCnDnEn的周长记为ln,则用含n的式子表示l1+l2+l3+…+ln为( )
如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数$y=\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…,An-1An都在x轴上(n是大于或等于2的正整数),若△P1OA2的内接正方形B1C1D1E2的周长记为l1,△P2A1A2的内接正方形B2C2D2E2的周长记为l2,…,△PnAn-1An的内接正方形BnCnDnEn的周长记为ln,则用含n的式子表示l1+l2+l3+…+ln为( )| A. | $\frac{8\sqrt{n}}{3}$ | B. | 2$\sqrt{n}$ | C. | $\frac{4\sqrt{n}}{3}$ | D. | $\frac{2\sqrt{n}}{3}$ |
17.在$\sqrt{2}$,-1,-3,0这四个实数中,最小的是( )
| A. | $\sqrt{2}$ | B. | -1 | C. | -3 | D. | 0 |
 =
= 时,求DE的长.
时,求DE的长.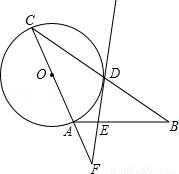
 某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:$\sqrt{3}$.
某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:$\sqrt{3}$. 如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E=15度.
如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=30°,则∠E=15度. (k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20
(k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20 ,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.
,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.