Question

2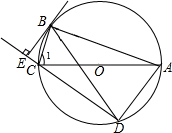．如图，⊙O是△ABC的外接圆，AC为直径，弦BD=BA，BE⊥DC交DC的延长线于点E．
（1）求证：∠1=∠BAD；
（2）求证：BE是⊙O的切线．

Answer 1

分析 （1）根据等腰三角形的性质和圆周角定理得出即可；
（2）连接BO，求出OB∥DE，推出EB⊥OB，根据切线的判定得出即可；

解答 证明：（1）∵BD=BA，
∴∠BDA=∠BAD，
∵∠1=∠BDA，
∴∠1=∠BAD；

（2）连接BO，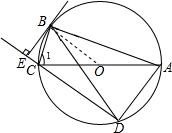
∵∠ABC=90°，
又∵∠BAD+∠BCD=180°，
∴∠BCO+∠BCD=180°，
∵OB=OC，
∴∠BCO=∠CBO，
∴∠CBO+∠BCD=180°，
∴OB∥DE，
∵BE⊥DE，
∴EB⊥OB，
∵OB是⊙O的半径，
∴BE是⊙O的切线．

点评 本题考查了三角形的外接圆与外心，等腰三角形的性质，切线的判定，熟练掌握切线的判定定理是解题的关键．