题目内容
下列图形能分成两个全等图形的是（）
A.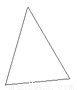 
B.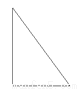 
C.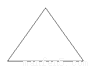 
D.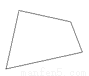 
C
【解析】全等图形需要大小相等，形状相同，原图中只有C是一个等腰三角形可以分成两个全等的直角三角形，A、B、D都不符合要求，
故选C.
练习册系列答案
相关题目
计算：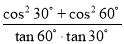 
+sin45°．
【解析】
试题分析：根据特殊角的三角函数值，可得实数的运算，根据实数的运算，可得答案．
试题解析：+sin45°
=
=2+
= 若等腰三角形的一边是7，另一边是4，则此等腰三角形的周长是（ ）.
A．18 B．15 C．18或15 D．无法确定
C.
【解析】
试题分析：分情况讨论，假设7作腰长，则三边分别为7，7，4，周长为18；假设4作腰长，则三边分别为4，4，7，周长为15，所以此等腰三角形的周长是18或15.
故选：C. 公路BC所在的直线恰为AD的垂直平分线，则下列说法中：①小明从家到书店与小颖从家到书店一样远；②小明从家到书店与从家到学校一样远；③小颖从家到书店与从家到学校一样远；④小明从家到学校与小颖从家到学校一样远. 正确的是（）
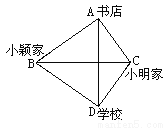
A. ①③ B. ②③ C. ②④ D. ③④
B
【解析】∵公路BC所在的直线恰为AD的垂直平分线，
∴ΔABC≌ΔDBC，
∴CA=CB，BA=BD，
故可判断出②小明从家到书店与从家到学校一样远；③小颖从家到书店与从家到学校一样远；
而无法判断出①小明从家到书店与小颖从家到书店一样远；④小明从家到学校与小颖从家到学校一样远，
故选B. 下列图中，与左图中的图案完全一致的是（）
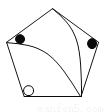
A. 
B.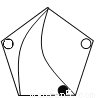 
C.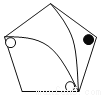 
D.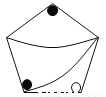 
A
【解析】A图案可以通过旋转得到，故A符合题意；B、C、D通过旋转、平移都不能得到，
故选A. 一个袋中装有2个红球，3个白球，和5个黄球，每个球除了顔色外都相同，从中任意摸出一个球，分别求出摸到红球，白球，黄球的概率。
，，
【解析】
试题分析：先求出球的总个数，根据概率的定义直接计算即可．概率=所求情况数与总情况数之比．
试题解析：摸到红球的概率为即，摸到白球的概率为
摸到白球的概率为，即 从分别标有1、2、3、4的四张卡片中，一次同时抽2张，其中和为奇数的概率是 ．
【解析】试题分析：如图所示，
由树状图可知共有4×3=12种可能，和为奇数的有8种，所以概率是＝．故答案为： ． 已知△ABC.求作：△A′B′C′，使△A′B′C′≌△ABC.
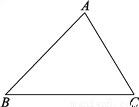
作图见解析
【解析】试题分析：本题可利用全等三角形的判定定理SSS作图，作AC=A′C′，A′B′=AB，BC=B′C′；根据全等三角形的判定可得△A′B′C′≌△ABC，注意尺规作图中作一条线段等于已知线段的作法．
试题解析：作法：①任意作一条射线B′M，以点B′为圆心，以BC为半径画弧，交射线于点C′；
②分别以点B′和点C′为圆心，以AB和AC为半径画弧，交于点A′，连接A... 如图，∠C＝∠D＝90°，若添加一个条件，可使用“HL”判定Rt△ABC与Rt△ABD全等，则以下给出的条件适合的是( )
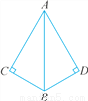
A. AC＝AD B. AB＝AB C. ∠ABC＝∠ABD D. ∠BAC＝∠BAD
A
【解析】根据题意可知∠C=∠D=90°，AB=AB，
然后由AC=AD，可根据HL判定两直角三角形全等，故符合条件；
而B答案只知道一边一角，不能够判定两三角形全等，故不正确；
C答案符合AAS，证明两三角形全等，故不正确；
D答案是符合AAS，能证明两三角形全等，故不正确.
故选：A.