题目内容
8.若关于x的方程x2+2nx+n2-3n+2=0有两个实数根x1、x2,则x1•x2+5n的最小值为$\frac{34}{9}$.分析 先根据判别式的意义得到得n≥$\frac{2}{3}$,再根据根与系数的关系得x1•x2=n2-3n+2,所以x1•x2+5n=n2-3n+2+5n,然后配方得到(n+1)2+1,再利用二次函数的性质确定x1•x2+5n的最小值.
解答 解:根据题意得△=4n2-4(n2-3n+2)≥0,解得n≥$\frac{2}{3}$,
∵x1•x2=n2-3n+2,
∴x1•x2+5n=n2-3n+2+5n
=n2+2n+2,
=(n+1)2+1,
∴当n≥$\frac{2}{3}$时,x1•x2+5n随n的增大而增大,
且n=$\frac{2}{3}$时,x1•x2+5n有最小值,最小值=($\frac{2}{3}$+1)2+1=$\frac{34}{9}$.
故答案为$\frac{34}{9}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式和二次函数的最值.

练习册系列答案
相关题目
18.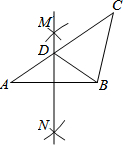 在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
 在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
19.函数$y=\frac{1}{{\sqrt{x-1}}}$中自变量的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x≥1 | D. | x≥-1 |
16.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )
| A. | $\frac{600}{x+50}=\frac{450}{x}$??????????????????????????????????????? | |
| B. | $\frac{600}{x-50}=\frac{450}{x}$??????????????????????????????????? | |
| C. | $\frac{600}{x}=\frac{450}{x+50}$????????????????????????????? | |
| D. | $\frac{600}{x}=\frac{450}{x-50}$??????????????????????????????? |
3.如果一个多边形的内角和等于720°,则这个多边形是( )
| A. | 四边形 | B. | 五边形 | C. | 六边形 | D. | 七边形 |
13.下列等式正确的是( )
| A. | a3÷a2=a3•a-2 | B. | (a2)3=a5 | C. | 2a2+a2=3a4 | D. | (a-b)2=a2-b2 |
20.如图,如图是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A多出4个“树枝”,图A4比图A3多出8个“树枝”,…,照此规律,图A6比图A2多出“树枝”( )
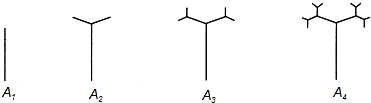

| A. | 64 | B. | 60 | C. | 56 | D. | 32 |
17. 如图,在方格纸上有一个三角形ABC,则这个三角形是( )
如图,在方格纸上有一个三角形ABC,则这个三角形是( )
 如图,在方格纸上有一个三角形ABC,则这个三角形是( )
如图,在方格纸上有一个三角形ABC,则这个三角形是( )| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 不能确定 |