题目内容
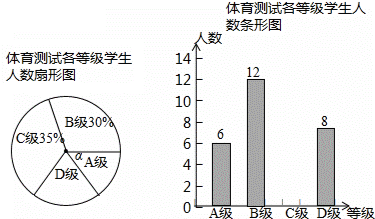
3.如果一个多边形的内角和等于720°,则这个多边形是( )| A. | 四边形 | B. | 五边形 | C. | 六边形 | D. | 七边形 |
分析 n边形的内角和可以表示成(n-2)•180°,设这个正多边形的边数是n,就得到方程,从而求出边数.
解答 解:这个正多边形的边数是n,则
(n-2)•180°=720°,
解得:n=6.
则这个正多边形的边数是6.
故选:C.
点评 考查了多边形内角和定理,此题比较简单,只要结合多边形的内角和公式,寻求等量关系,构建方程求解.

练习册系列答案
相关题目
13.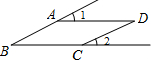 如图,∠1=∠B,∠2=25°,则∠D=( )
如图,∠1=∠B,∠2=25°,则∠D=( )
 如图,∠1=∠B,∠2=25°,则∠D=( )
如图,∠1=∠B,∠2=25°,则∠D=( )| A. | 25° | B. | 45° | C. | 50° | D. | 65° |
11.已知a、b、c为非零实数,且满足$\frac{b+c}{a}=\frac{a+b}{c}=\frac{a+c}{b}=k$,则一次函数y=kx+k+1的图象一定经过( )
| A. | 第一、二、三象限 | B. | 第二、四象限 | C. | 第一象限 | D. | 第二象限 |
15.下列几何体中左视图是矩形的共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.下列选项中,可以用来证明命题“若|a-1|>1,则a>2”是假命题的反例是( )
| A. | a=2 | B. | a=1 | C. | a=0 | D. | a=-1 |
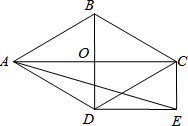 如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.