题目内容
18.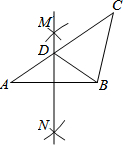 在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )
在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
分析 首先根据作图过程得到MN垂直平分AB,然后利用中垂线的性质得到∠A=∠ABD,然后利用三角形外角的性质求得∠CDB的度数,从而可以求得∠C的度数.
解答 解:∵根据作图过程和痕迹发现MN垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=35°,
∵CD=BC,
∴∠CDB=∠CBD=2∠A=70°,
∴∠C=40°,
故选A.
点评 本题考查了基本作图中作已知线段的垂直平分线及线段的垂直平分线的性质,解题的关键是能利用垂直平分线的性质及外角的性质进行角之间的计算,难度不大.

练习册系列答案
相关题目
13.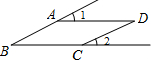 如图,∠1=∠B,∠2=25°,则∠D=( )
如图,∠1=∠B,∠2=25°,则∠D=( )
 如图,∠1=∠B,∠2=25°,则∠D=( )
如图,∠1=∠B,∠2=25°,则∠D=( )| A. | 25° | B. | 45° | C. | 50° | D. | 65° |
10.某学习小组设计了一个摸球试验,在袋中装有黑,白两种颜色的球,这些球的形状大小质地等完全相同,即除颜色外无其他差别.在看不到球的情况下,随机从袋中摸出一个球,记下颜色,再把它放回,不断重复.下表是由试验得到的一组统计数据:
从这个袋中随机摸出一个球,是白球的概率约为0.6.(结果精确到0.1)
| 摸球的次数 | 100 | 200 | 300 | 400 | 500 | 600 |
| 摸到白球的次数 | 58 | 118 | 189 | 237 | 302 | 359 |
| 摸到白球的频率 | 0.58 | 0.59 | 0.63 | 0.593 | 0.604 | 0.598 |
7. 如图是某一正方体的展开图,那么该正方体是( )
如图是某一正方体的展开图,那么该正方体是( )
 如图是某一正方体的展开图,那么该正方体是( )
如图是某一正方体的展开图,那么该正方体是( )| A. |  | B. |  | C. |  | D. |  |
 秒1个单位的速度向右平移,经过3秒该直线可将?OABC的面积平分.
秒1个单位的速度向右平移,经过3秒该直线可将?OABC的面积平分.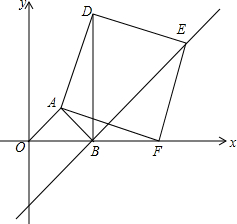 如图,正方形OABC的顶点A在第一象限,B点坐标为(2,0),正方形ADEF顶点F坐标为(4,0).
如图,正方形OABC的顶点A在第一象限,B点坐标为(2,0),正方形ADEF顶点F坐标为(4,0).