题目内容
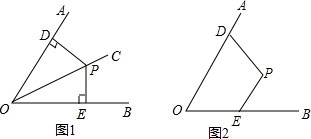
 如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角有(不含∠1)
如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角有(不含∠1)考点:平行线的性质
专题:
分析:由平行线的性质可得到∠1=∠HEF=∠AHE=∠GHC=∠HCF=∠DAC,结合∠DAH+∠AHG=180°,可求得∠AHG.
解答:解:
∵EF∥AC,
∴∠1=∠HCF,∠FEH=∠AHE,
∵EG∥BC,
∴∠1=∠FEH,∠GHC=∠HCF,
∴AD∥BC,
∴∠DAH=∠HCF,
∴∠1=∠HEF=∠AHE=∠GHC=∠HCF=∠DAC,
即和∠1相等的角有5个;
当∠1=40°时,则∠DAC=∠1=40°,
∵AD∥EG,
∴∠DAC+∠AHG=180°,
∴∠AHG=180°-40°=140°;
故答案为:5;140°.
∵EF∥AC,
∴∠1=∠HCF,∠FEH=∠AHE,
∵EG∥BC,
∴∠1=∠FEH,∠GHC=∠HCF,
∴AD∥BC,
∴∠DAH=∠HCF,
∴∠1=∠HEF=∠AHE=∠GHC=∠HCF=∠DAC,
即和∠1相等的角有5个;
当∠1=40°时,则∠DAC=∠1=40°,
∵AD∥EG,
∴∠DAC+∠AHG=180°,
∴∠AHG=180°-40°=140°;
故答案为:5;140°.
点评:本题主要考查平行线的性质,掌握平行线的性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补.

练习册系列答案
相关题目
 如图所示的图形面积最适合表示一个公式,这个公式是( )
如图所示的图形面积最适合表示一个公式,这个公式是( )| A、a2-b2=a(a-b)+b(a-b) |
| B、(a+b)2=a2+2ab+b2 |
| C、(a-b)2=a2-2ab+b2 |
| D、a2-b2=(a+b)(a-b) |
若am+1b3和(n-1)a2b3与是同类项,且它们合并后结果是0,则( )
| A、m=2,n=2 |
| B、m=1,n=2 |
| C、m=2,n=0 |
| D、m=1,n=0 |
 如图,已知△ABC中,AC=BD,∠DAC=30°,∠ACB=40°,求∠ABC的度数.
如图,已知△ABC中,AC=BD,∠DAC=30°,∠ACB=40°,求∠ABC的度数.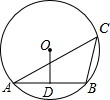 如图所示,已知△ABC内接于⊙O,∠C=45°,点O到弦AB的距离OD=2,求:
如图所示,已知△ABC内接于⊙O,∠C=45°,点O到弦AB的距离OD=2,求: 如图,在等腰三角形ABC中,请根据图中所给数据求出tanB.
如图,在等腰三角形ABC中,请根据图中所给数据求出tanB.