题目内容
已知点P在∠AOB内,点D,E分别在边OA,OB上.
(1)如图1,若∠PDO=90°,∠PEO=90°,且PD=PE,求证:点P在∠AOB的平分线上;
(2)如图2,若∠PDO+∠PEO=180°,且PD=PE,问:点P是否在∠AOB的平分线上?试证明你的结论.
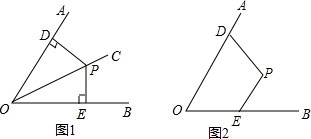
(1)如图1,若∠PDO=90°,∠PEO=90°,且PD=PE,求证:点P在∠AOB的平分线上;
(2)如图2,若∠PDO+∠PEO=180°,且PD=PE,问:点P是否在∠AOB的平分线上?试证明你的结论.

考点:角平分线的性质
专题:
分析:(1)利用“HL”证明Rt△ODP和Rt△OEP全等,根据全等三角形对应角相等可得∠DOP=∠EOP,再根据角平分线的定义证明;
(2)过点P作PF⊥OA于F,作PG⊥OB于G,先求出∠DPE=∠FPG,再求出∠DPF=∠EPG,然后利用“角角边”证明△PDF和△PEG全等,根据全等三角形对应边相等可得PF=PG,再根据到角的两边距离相等的点在角的平分线上解答.
(2)过点P作PF⊥OA于F,作PG⊥OB于G,先求出∠DPE=∠FPG,再求出∠DPF=∠EPG,然后利用“角角边”证明△PDF和△PEG全等,根据全等三角形对应边相等可得PF=PG,再根据到角的两边距离相等的点在角的平分线上解答.
解答:(1)证明:在Rt△ODP和Rt△OEP中,
,
∴Rt△ODP≌Rt△OEP(HL),
∴∠DOP=∠EOP,
∴点P在∠AOB的平分线上;
(2)解:如图,过点P作PF⊥OA于F,作PG⊥OB于G,
∴∠FPG+∠O=180°,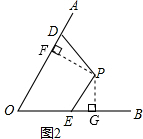
∵∠PDO+∠PEO=180°,
∴∠DPE+∠O=180°,
∴∠DPE=∠FPG,
∴∠DPF=∠EPG,
在△PDF和△PEG中,
,
∴△PDF≌△PEG(AAS),
∴PF=PG,
又∵PF⊥OA,PG⊥OB,
∴点P在∠AOB的平分线上.
|
∴Rt△ODP≌Rt△OEP(HL),
∴∠DOP=∠EOP,
∴点P在∠AOB的平分线上;
(2)解:如图,过点P作PF⊥OA于F,作PG⊥OB于G,
∴∠FPG+∠O=180°,

∵∠PDO+∠PEO=180°,
∴∠DPE+∠O=180°,
∴∠DPE=∠FPG,
∴∠DPF=∠EPG,
在△PDF和△PEG中,
|
∴△PDF≌△PEG(AAS),
∴PF=PG,
又∵PF⊥OA,PG⊥OB,
∴点P在∠AOB的平分线上.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,到角的两边距离相等的点在角的平分线上的证明,全等三角形的判定与性质,熟记性质并理解证明方法是解题的关键.

练习册系列答案
相关题目
下列算式中正确的是( )
| A、(-0.001)0=-1 | ||
| B、(a2b5)5÷(-ab2)10=b5 | ||
C、(4x)-2=
| ||
| D、3.24×10-3=0.000324 |
 用3个相同的立方块搭成的几何体如图所示,则它的俯视图是( )
用3个相同的立方块搭成的几何体如图所示,则它的俯视图是( )A、 |
B、 |
C、 |
D、 |
 如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角有(不含∠1)
如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角有(不含∠1) 如图,在△ABC中,∠ACB=90°,BD是∠ABC的平分线,E为AB边上一点,且CE⊥BD,垂足为O,求证:
如图,在△ABC中,∠ACB=90°,BD是∠ABC的平分线,E为AB边上一点,且CE⊥BD,垂足为O,求证: 下图是一个长方形纸片,长为5a2+4b2,宽为6a2,在它的四个角上都剪去一个边长为
下图是一个长方形纸片,长为5a2+4b2,宽为6a2,在它的四个角上都剪去一个边长为