题目内容
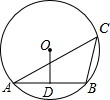 如图所示,已知△ABC内接于⊙O,∠C=45°,点O到弦AB的距离OD=2,求:
如图所示,已知△ABC内接于⊙O,∠C=45°,点O到弦AB的距离OD=2,求:(1)弦AB的长;
(2)弦AB所对劣弧的长.
考点:圆周角定理,等腰直角三角形,弧长的计算
专题:
分析:(1)连接OA、OB,根据圆周角定理,易得∠AOB=90°,则△OAB是等腰直角三角形,由此可求出弦AB的长;
(2)先由△OAD是等腰直角三角形求出OA的长,再利用弧长公式即可求解.
(2)先由△OAD是等腰直角三角形求出OA的长,再利用弧长公式即可求解.
解答: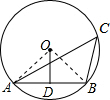 解:(1)连接OA,OB,则OA=OB,∠AOB=2∠C;
解:(1)连接OA,OB,则OA=OB,∠AOB=2∠C;
∵∠C=45°,
∴∠AOB=90°,
∴△OAB是等腰直角三角形,
∵点O到弦AB的距离OD=2,
∴AB=2OD=4;
(2)∵OD=2,AD=2,∠ODA=90°,
∴OA=
OD=2
,
∴弦AB所对劣弧的长为
=
π.
 解:(1)连接OA,OB,则OA=OB,∠AOB=2∠C;
解:(1)连接OA,OB,则OA=OB,∠AOB=2∠C;∵∠C=45°,
∴∠AOB=90°,
∴△OAB是等腰直角三角形,
∵点O到弦AB的距离OD=2,
∴AB=2OD=4;
(2)∵OD=2,AD=2,∠ODA=90°,
∴OA=
| 2 |
| 2 |
∴弦AB所对劣弧的长为
90π×2
| ||
| 180 |
| 2 |
点评:此题考查的是圆周角定理,等腰直角三角形的判定与性质,弧长的计算.能够由圆周角定理正确的判断出△OAB的形状是解答此题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
下面是一组按规律排列的数:1,2,4,8,16,…,则第2008个数是( )
| A、22009 |
| B、22008 |
| C、22007 |
| D、22006 |
下列算式中正确的是( )
| A、(-0.001)0=-1 | ||
| B、(a2b5)5÷(-ab2)10=b5 | ||
C、(4x)-2=
| ||
| D、3.24×10-3=0.000324 |
 请从(1)和(2)两道试题任选一题作答,如果两题都做,默认第一题.
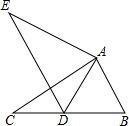
请从(1)和(2)两道试题任选一题作答,如果两题都做,默认第一题. 如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角有(不含∠1)
如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角有(不含∠1)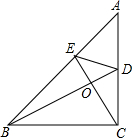 如图,在△ABC中,∠ACB=90°,BD是∠ABC的平分线,E为AB边上一点,且CE⊥BD,垂足为O,求证:
如图,在△ABC中,∠ACB=90°,BD是∠ABC的平分线,E为AB边上一点,且CE⊥BD,垂足为O,求证: 已知,如图,平行四边形ABCD中,∠BDC的平分线DE交直线AB于E,取DE中点M并连接CM、BM.
已知,如图,平行四边形ABCD中,∠BDC的平分线DE交直线AB于E,取DE中点M并连接CM、BM.