题目内容

抛物线y=-x2-3x+3与y轴交点的坐标为
 
．
考点：二次函数图象上点的坐标特征
专题：
分析：把x=0代入抛物线y=-x2-3x+3，即得抛物线y=-x2-3x+3与y轴的交点．
解答：解：∵当x=0时，抛物线y=-x2-3x+3与y轴相交，
∴把x=0代入y=-x2-3x+3，求得y=3，
∴抛物线y=-x2+3x-3与y轴的交点坐标为（0，3）．
故答案为（0，3）．
点评：本题考查了二次函数图象上点的坐标特征，比较简单，掌握y轴上点的横坐标为0是解题的关键．
练习册系列答案
相关题目
某中学课外活动小组准备围建一个矩形生物苗圃园，其中一边靠墙，另外三边用长为50米的篱笆围成．已知墙长为26米（如图所示），设这个苗圃园平行于墙的一边的长为x米．
（1）若垂直于墙的一边长为y米，直接写出y与x的函数关系式及其自变量x的取值范围；
（2）当x为多少米时，这个苗圃园的面积最大，并求出这个最大值；
（3）当这个苗圃园的面积不小于300平方米时，试结合函数图象，求出x的取值范围．
“知识改变命运，科技繁荣祖国”．我市中小学每年都要举办一届科技运动会．如图为我市某校2012年参加科技运动会航模比赛（包括空模、海模、车模、建模四个类别）的参赛人数统计图：
（1）该校参加车模、建模比赛的人数分别是
 
人和
 
人；
（2）该校参加航模比赛的总人数是
 
人；
（3）空模所在扇形的圆心角的度数是
 
°，并把条形统计图补充完整：（温馨提示：作图时别忘了用0.5毫米及以上的黑色签字笔涂黑）；
（4）从全市中小学参加航模比赛选手中随机抽取80人，其中有32人获奖．今年我市中小学参加航模比赛人数共有2100人，请你估算今年参加航模比赛的获奖人数约是多少人？
在Rt△ABC，∠C=90°，AC=4，AB=5，则tanB=
 
．
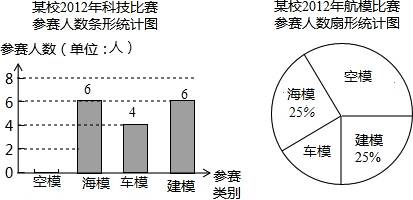
如图，已知AB∥CD∥EF，它们依次交直线l1、l2于点A、D、F和点B、C、E，如果AD=6，DF=3，BC=5，那么BE=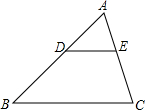
 
．
如图，在△ABC中，DE∥BC，DE与边AB相交于点D，与边AC相交于点E，如果AD=3，BD=4，AE=2，那么AC=
 
．
在Rt△ABC中，∠A=90°，AC=5，BC=13，那么tanB的值是（　　）
A、
5
12
B、
12
5
C、
12
13
D、
5
13
已知⊙P在直角坐标平面内，它的半径是5，圆心P（-3，4），则坐标原点O与⊙P的位置关系是
 
．
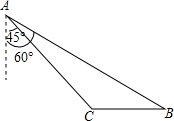如图所示，2013年4月10日，中国渔民在中国南海huangyandao附近捕鱼作业，中国海监渔船在A第侦察发现，在东南偏东60°方向的B地，有一艘某国军舰正以每小时13海里的速度向正西方方向的C地行驶，企图抓捕正在C地捕鱼的中国渔民．此时，C地位于中国海监船的南偏东45°方向的10海里处，中国海监船以每小时30海里的速度赶往C地救援我国渔民，能不能及时赶到？（
2
≈1.41，
3
≈1.73，
6
≈2.45）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网