题目内容

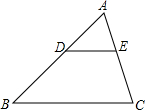如图，在△ABC中，DE∥BC，DE与边AB相交于点D，与边AC相交于点E，如果AD=3，BD=4，AE=2，那么AC=
 
．
考点：平行线分线段成比例
专题：
分析：由平行可得到
AD
BD
=
AE
EC
，代入可求得EC，再利用线段的和可求得AC．
解答：解：∵DE∥BC，
∴
AD
DB
=
AE
EC
，即
3
4
=
2
EC
，
解得EC=
8
3
，
∴AC=AE+EC=2+
8
3
=
14
3
，
故答案为：
14
3
．
点评：本题主要考查平行线分线段成比例，掌握平行线分线段所得线段对应成比例是解题的关键．
练习册系列答案
相关题目
已知：抛物线y=x2-2（m+2）x+m2-1与x轴有两个交点．
（1）求m的取值范围；
（2）当m为非正整数时，关于x的一元二次方程x2-2（m+2）x+m2-1有整数根，求m的值．
已知二次函数y=kx2-（k+3）x+3在x=0和x=4时的函数值相等．
（1）求该二次函数的表达式；
（2）画出该函数的图象，并结合图象直接写出当y＜0时，自变量x的取值范围；
（3）已知关于x的一元二次方程k2x2-
3
mx+m2-m=0，当-1≤m≤3时，判断此方程根的情况．
如图，正方形DEFG内接于Rt△ABC，∠C=90°，AE=4，BF=9，则tanA=
 
．
抛物线y=-x2-3x+3与y轴交点的坐标为
 
．
如图，△ABC中，以BC为直径的圆交AB于点D，∠ACD=∠ABC．
（1）求证：CA是圆的切线；
（2）若点E是BC上一点，已知EC=4，∠ABC=32°，∠AEC=67°，求圆的直径BC的长．（精确到1）
如果二次函数y=（m-1）x2+5x+m2-1的图象经过原点，那么m=
 
．
已知3x=2y，那么下列等式一定成立的是（　　）
A、x=2，y=3
B、
x
y
=
3
2
C、
x
y
=
2
3
D、3x+2y=0
如图，边长为2菱形ABCD中，∠DAB=60°，连接对角线AC，以AC为边作第二个菱形ACC1D1，使∠D1AC=60°；连接AC1，再以AC1为边作第三个菱形AC1C2D2，使∠D2AC1=60°；…，按此规律所作的第6个菱形的边长为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网