题目内容
4.定义:a是不为1的有理数,我们把$\frac{1}{1-a}$称为a的差倒数.如:2的差倒数是$\frac{1}{1-2}=-1$,-1的差倒数是$\frac{1}{{1-({-1})}}=\frac{1}{2}$.已知a1=-$\frac{1}{3}$,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2016=4.分析 利用规定的运算方法,分别算得a1,a2,a3,a4…找出运算结果的循环规律,利用规律解决问题.
解答 解:∵a1=-$\frac{1}{3}$,
a2=$\frac{1}{1-(-\frac{1}{3})}$=$\frac{3}{4}$,
a3=$\frac{1}{1-\frac{3}{4}}$=4,
a4=$\frac{1}{1-4}$=-$\frac{1}{3}$,
…
∴数列以-$\frac{1}{3}$,$\frac{3}{4}$,4三个数依次不断循环,
∵2016÷3=672,
∴a2016=a3=4.
故答案为:4.
点评 此题考查数字的变化规律,找出数字之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
9.如果有理数a=5.93×1012,则a的整数部分的位数是( )
| A. | 13 | B. | 12 | C. | 14 | D. | 11 |
9.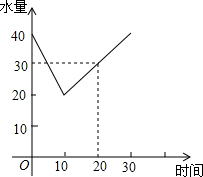 一蓄水池中有水40m3,水池里的水量与放水时间有如下关系:
一蓄水池中有水40m3,水池里的水量与放水时间有如下关系:
设放水时间为x(分钟),水池中的水量为y(m3).
(1)请直接写出y与x的关系式;
(2)当放水时间为10分钟时,求出此时水池中的水量;当水池中的水刚被放完时,经过了多少分钟?
(3)当放水10分钟后,再开放一个进水管(此时,放水与进水同时进行),则水池中的水量随着时间的变化如图所示,请根据图象求出进水管每分钟放进多少水量?
 一蓄水池中有水40m3,水池里的水量与放水时间有如下关系:
一蓄水池中有水40m3,水池里的水量与放水时间有如下关系:| 放水时间/分 | 2 | 4 | 6 | 8 | … |
| 水池中水量/m3 | 36 | 32 | 28 | 24 | … |
(1)请直接写出y与x的关系式;
(2)当放水时间为10分钟时,求出此时水池中的水量;当水池中的水刚被放完时,经过了多少分钟?
(3)当放水10分钟后,再开放一个进水管(此时,放水与进水同时进行),则水池中的水量随着时间的变化如图所示,请根据图象求出进水管每分钟放进多少水量?
16.将正整数依次按下表规律排成四列,则根据表中的排列规律,数2015应排的位置是第675行第3列
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | |
| 第2行 | 6 | 5 | 4 | |
| 第3行 | 7 | 8 | 9 | |
| 第4行 | 12 | 11 | 10 | |
| … |
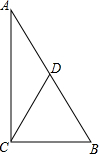 如图,Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm,点D是AB的中点,则cos∠ACD=$\frac{4}{5}$.
如图,Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm,点D是AB的中点,则cos∠ACD=$\frac{4}{5}$. 已知一次函数y=kx+b的图象如图所示,则关于x的不等式k(x+2)+2b>0的解集为x>-8.
已知一次函数y=kx+b的图象如图所示,则关于x的不等式k(x+2)+2b>0的解集为x>-8.