题目内容
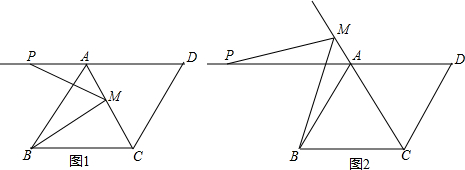
15.如图,过点A作△ABC中∠B、∠C的外角平分线的垂线,垂足分别为M、N,联结MN.(1)求证:MN∥BC;
(2)若设AB=c,BC=a,AC=b,则用a、b、c的代数式表示MN的长;
(3)如图②、③中,MN与a、b、c的关系还成立吗?若成立,请说明理由;若不成立,请求出新的关系式.
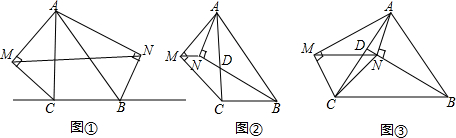
分析 (1)延长AM交BC的延长线于E,延长AN交CB的延长线于F,根据等腰三角形的三线合一、三角形的中位线定理解答即可;
(2)根据(1)的结论结合图形解得即可;
(3)延长AM交BC的延长线于E,延长AN交CB于F,根据等腰三角形的三线合一、三角形的中位线定理解答即可.
解答 解:如图①,延长AM交BC的延长线于E,延长AN交CB的延长线于F,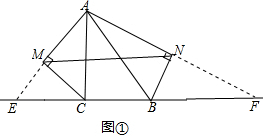
(1)∵CM为∠ACE的平分线,CM⊥AM,∴AM=ME,CA=CE,
同理,AN=NF,BF=BA,
∴MN是三角形AEF的中位线,
∴MN∥BC;
(2)EF=EC+BC+BF=CA+BC+AB=a+b+c,
∴MN=$\frac{1}{2}$(a+b+c);
(3)如图②,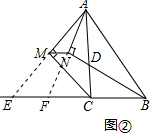
由(1)得,MN=$\frac{1}{2}$(a+b-c);
如图③,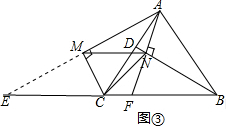
MN=$\frac{1}{2}$(a+b-c).
点评 本题考查的是三角形的中位线定理和三角形的性质,掌握三角形的中位线平行于第三边且等于第三边的一半、等腰三角形的三线合一是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目

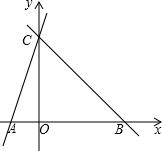 如图,直线y=kx+k交x轴、y轴分别于A,C,直线BC过点C交x轴于B,OC=3OA,∠CBA=45°.
如图,直线y=kx+k交x轴、y轴分别于A,C,直线BC过点C交x轴于B,OC=3OA,∠CBA=45°. 将如图中△ABC作下列变化,画出相应的图形:
将如图中△ABC作下列变化,画出相应的图形: