题目内容
2.如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在y轴和x轴的正半轴上,且AO=5、OC=10.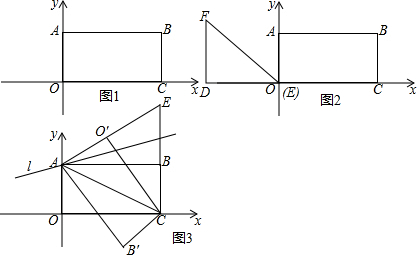
(1)在坐标平面内将此矩形绕原点O逆时针旋转m(0<m<360)度后,如果点C恰好落在直线AB上,那么m=150°或30°.
(2)在图(2)中,Rt△DEF,∠D=90°,DE=DF=6,DE边在x轴上且E点与原点重合,将Rt△DEF沿x轴的正方向以每秒1个单位的速度平移,当点E与点C重合时停止运动,设平移的时间为t,Rt△DEF与矩形OABC重叠部分的面积为y,求在平移过程中y与t的函数关系式.
(3)如图(3)把△OAC沿直线AC折叠后点O落在点O′处,延长AO′与线段CB的延长线交于点E,再把△ABC沿直线AC折叠后点B落在点B′处,连接B′E,
①求△AB′E的面积;
②过点A任作直线l交线段EB′于点P,E、B′到直线l的距离分别为d1、d2,试求d1+d2的最大值.
分析 (1)先画出图形,C点C恰好落在直线AB上(有C′和C″两点),在Rt△C′AO中,求出∠AC′O=30°,根据矩形的性质得出AB∥OC,求出∠C′OC+∠AC′O=180°,∠C′C″O=∠COC″,即可得出答案;
(2)分为三种情况:当0<t≤5时,②当5<t≤6时,③当6<t≤10时,画出图形,求出重叠部分面积即可;
(3)求出AE=EC,设AE=x,则EB=x-5,在Rt△EBA中,由勾股定理得出x2=102+(x-5)2,求出AE=12.5,即可求出答案;过B′作B′M⊥AP于M,过E作EN⊥AP于N,EG⊥B′M于G,得出当G和E重合时,d1+d2的值最大,求出B′E长即可.
解答 解:(1)如图1,C点C恰好落在直线AB上(有C′和C″两点),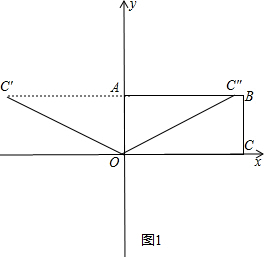
∵在Rt△C′AO中,∠C″AO=90°,OC″=OC=10,OA=5,
∴∠AC′O=30°,
∵四边形AOCB是矩形,
∴AB∥OC,
∴∠C′OC+∠AC′O=180°,∠C′C″O=∠COC″,
∴∠C′OC=150°,
∵OC′=OC″=OC=10,
∴∠AC″O=∠C′=30°,
∴∠COC″=∠AC″O=30°,
即m=150°或30°,
故答案为:150°或30°;
(2)分为三种情况:
①当0<t≤5时,如图2,设EF交OA于Q,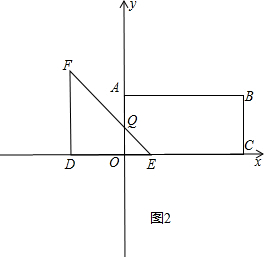
∵DF=DE,∠FDE=90°,
∴∠FED=45°,
∵四边形AOCB是矩形,
∴∠AOC=90°,
∴∠OQE=∠FEO=45°,
∴OQ=OE=t×1=t,
∴重叠部分的面积S=S△QOE=$\frac{1}{2}$t•t=$\frac{1}{2}$t2;
②当5<t≤6时,如图3,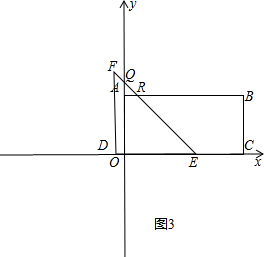
由①知:OE=OQ=t,
∵四边形AOCB是矩形,
∴AB∥OC,∠QAB=90°,
∴∠∠QRA=∠FED=45°,
∴∠AQR=∠QRA=45°,
∴AR=AQ=t-5,
∴重叠部分的面积S=S梯形AOER=$\frac{1}{2}$×(AR+OE)×OA=$\frac{1}{2}$•(t-5+t)•5,
即S=5t-12.5;
③当6<t≤10时,如图4,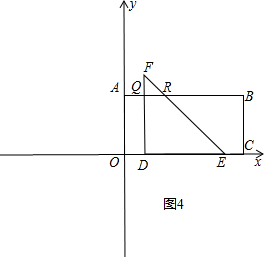
∵QF=QR=6-5=1,
∴重叠部分的面积S=$\frac{1}{2}$×(QR+DE)×DQ=$\frac{1}{2}×$(1+6)×5=17.5;
(3)如图5,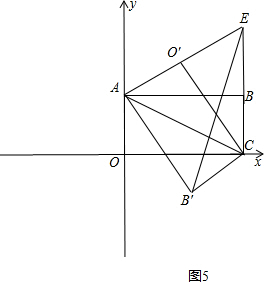
∵四边形AOCB是矩形,
∴∠OAB=90°,
∵根据折叠的性质得出AB=AB′=10,∠OAC=∠EAC,∠BAC=∠B′AC,
∴∠EAB′=∠EAC+∠B′AC=∠OAC+∠BAC=∠OAB=90°,
∵四边形AOCB是矩形,
∴OA∥BC,
∴∠ECA=∠OAC,
∵∠OAC=∠EAC,
∴∠EAC=∠ECA,
∴AE=EC,
设AE=x,则EB=x-5,
在Rt△EBA中,由勾股定理得:x2=102+(x-5)2,
解得:x=12.5,
即AE=12.5,
∴△AB′E的面积的面积是:$\frac{1}{2}$×AB′×AE=$\frac{1}{2}×$10×12.5=62.5;
如图6,过B′作B′M⊥AP于M,过E作EN⊥AP于N,EG⊥B′M于G,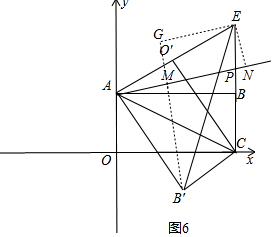
∠G=∠GMN=∠ENM=90°,
则四边形EGMN是矩形,
所以MG=EN=d1,B′M=d2,
所以d1+d2=B′G,
当G和E重合时,d1+d2的值最大,最大值是$\sqrt{1{0}^{2}+12.{5}^{2}}$=$\frac{5\sqrt{41}}{2}$.
点评 本题考查了折叠的性质,矩形的性质,等腰三角形的性质等知识点的应用,能综合运用性质进行推理是解此题的关键,综合性比较强,难度偏大.

 寒假学与练系列答案
寒假学与练系列答案 如图,是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数是5或6或7或8或9或10.
如图,是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数是5或6或7或8或9或10. 如图,在△ABC中,D是BC上一点,且满足AC=AD,请你说明AB2=AC2+BC•BD.
如图,在△ABC中,D是BC上一点,且满足AC=AD,请你说明AB2=AC2+BC•BD.
 如图,在矩形ABCD中,AB=5,BC=13,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则cos∠FBC的值为$\frac{5\sqrt{26}}{26}$.
如图,在矩形ABCD中,AB=5,BC=13,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则cos∠FBC的值为$\frac{5\sqrt{26}}{26}$. 如图,已知反比例函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过点A(1,5),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
如图,已知反比例函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过点A(1,5),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.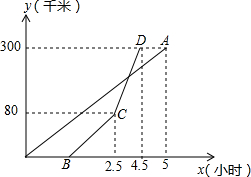 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B-C-D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.下列四种说法:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B-C-D表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.下列四种说法: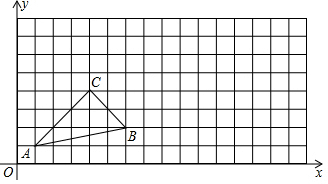 如图,△ABC中顶点A(1,1),B(6,2),C(4,4),将△ABC向右平移5个单位得到△A1B1C1,将△A1B1C1绕点B1顺时针方向旋转90°得到△A2B2C2.
如图,△ABC中顶点A(1,1),B(6,2),C(4,4),将△ABC向右平移5个单位得到△A1B1C1,将△A1B1C1绕点B1顺时针方向旋转90°得到△A2B2C2.