题目内容
14. 如图,已知反比例函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过点A(1,5),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.
如图,已知反比例函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过点A(1,5),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.(1)写出反比例函数解析式;
(2)若四边形ABMN是平行四边形,求AB所在直线的解析式;
(3)当点B在双曲线上移动时,试判断直线AB与直线MN的位置关系,并说明理由.
分析 (1)根据待定系数法,可得函数解析式;
(2)根据平行四边形的性质可得C点坐标,根据AC平行于y轴,可得m的值,根据待定系数法,可得答案;
(3)根据平行线间的性质:一次项的系数相等,可得答案.
解答 解:(1)将A(1,5)代入反比例函数y=$\frac{k}{x}$,得
$\frac{k}{1}$=5.解得k=5,
反比例函数y=$\frac{5}{x}$;
(2)由四边形ABMN是平行四边形,得
NC=CB,MC=AC.
由AM⊥x轴,垂足为M,BN⊥y轴,得
C($\frac{m}{2}$,n)还可以表示为(1,$\frac{5}{2}$).
$\frac{m}{2}$=1,n=$\frac{5}{2}$.
解得m=2,n=$\frac{5}{2}$,即B(2,$\frac{5}{2}$),
设直线AB的解析式为y=kx+b,
将A(1,5),B(2,$\frac{5}{2}$)代入函数解析式,得
$\left\{\begin{array}{l}{k+b=5}\\{2k+b=\frac{5}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{5}{2}}\\{b=\frac{15}{2}}\end{array}\right.$,
直线AB的解析式为y=-$\frac{5}{2}$x+$\frac{15}{2}$;
(3)AB∥MN,理由如下:
由AM⊥x轴,垂足为M,BN⊥y轴,得
M(1,0),N(0,n).
直线MN一次项的系数为$\frac{0-n}{1-0}$=-n,
直线AB一次项系数为$\frac{n-5}{m-1}$=$\frac{n-5}{\frac{5}{n}-1}$=$\frac{(n-5)n}{5-n}$=-n,
∴AB∥MN.
点评 本题考查了反比例函数综合题,(1)利用待定系数法求函数解析式,(2)平行四边形的性质得出C点坐标是解题关键,(3)利用平行线间的一次项系数相等是解题关键.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案| A. | -3.14是负数,不是分数 | |
| B. | 有理数不是负数就是正数 | |
| C. | 没有最大的负整数 | |
| D. | -2000既是负数,也是整数,还是有理数 |
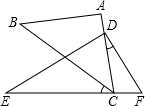 将一副直角三角板如图摆放,点C在EF上,AC经过点D,∠A=∠EDF=90°,∠BCE=40°,则∠CDF=25°.
将一副直角三角板如图摆放,点C在EF上,AC经过点D,∠A=∠EDF=90°,∠BCE=40°,则∠CDF=25°.