��Ŀ����
19����ͼ��CΪ�߶�AB���е㣬��P�ӵ�A������acm/s���ٶ���AB���B�˶���ͬʱ����Q�ӵ�B������bcm/s��b��a�����ٶ���BA���A�˶�����Q�˶���ʱ��Ϊt s����P���Q�ڵ�D������AB=6CD����1����$\frac{b}{a}$��ֵ��
��2����EΪBQ���е㣬��t=4����P��Q���˶��Ĺ����У�ʱ��PB=44cm��CE=26cm����AB����aֵ��
��3���ڣ�2���������£�����P���E����ʱ����Pֹͣ�˶����ڵ�P���E������ʱ�̣���R�ӵ�D������3cm/s���ٶ���DA��A�˶�����Pֹͣ�˶���tΪ��ֵʱ��RQ=$\frac{1}{2}$PE��
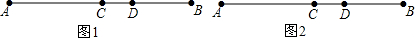
���� ��1������·��=�ٶȡ�ʱ�䣬��֪ʱ����ͬʱ���ٶ�֮�ȵ���·��֮�ȣ��ɵ�P���Q�ڵ�D�������ó�$\frac{b}{a}$=$\frac{\frac{BD}{t}}{\frac{AD}{t}}$=$\frac{BD}{AD}$��Ȼ�������е�Ķ����Լ�AB=6CD���㼴����⣻
��2���ɵ�EΪBQ���е㣬�ɵ�BE=$\frac{1}{2}$BQ����t=4ʱ��PB=AB-AP=AB-4a=AB-8b=44�٣�CE=BC-BE=$\frac{1}{2}$AB-$\frac{1}{2}$��4b=$\frac{1}{2}$AB-2b=26�ڣ�������������������AB��b�Ķ�Ԫһ�η����飬������⣻
��3���ڣ�2���������£��������P���E����ʱ����ʱ��Ϊ12s����BP=BE=12���������P���Q�ڵ�D��������ʱ��Ϊ10s����ʱBD=20cm��Ȼ�����������������ۣ���R��Q�ĺ��棻��R��Q��ǰ�森������RQ=$\frac{1}{2}$PE�г�����t�ķ��̣��ⷽ�̼�����⣮
��� �⣺��1����CΪ�߶�AB���е㣬AB=6CD��
��AC=BC=$\frac{1}{2}$AB=3CD��
�ߵ�P�ӵ�A������acm/s���ٶ���AB���B�˶���ͬʱ����Q�ӵ�B������bcm/s��b��a�����ٶ���BA���A�˶�����Q�˶���ʱ��Ϊts����P���Q�ڵ�D������
��AD=at��BD=bt��
��$\frac{b}{a}$=$\frac{\frac{BD}{t}}{\frac{AD}{t}}$=$\frac{BD}{AD}$=$\frac{BC-CD}{AC+CD}$=$\frac{3CD-CD}{3CD+CD}$=$\frac{2}{4}$=$\frac{1}{2}$��
��2���ߵ�EΪBQ���е㣬
��BE=$\frac{1}{2}$BQ��
��t=4ʱ��PB=AB-AP=AB-4a=AB-8b=44�٣�
CE=BC-BE=$\frac{1}{2}$AB-$\frac{1}{2}$��4b=$\frac{1}{2}$AB-2b=26�ڣ�
��������������AB=60��b=2��
��AB=60cm��a=2b=4cm/s��
��3����AB=60cm��a=4cm/s��b=2cm/s��
���P���E����ʱ����ʱ��Ϊxs��
��AP+BE=AB��
��4x+$\frac{1}{2}$��2x=60��
���x=12��
BP=BE=12��
��P���Q�ڵ�D��������ʱ��Ϊ��$\frac{60}{4+2}$=10��s������ʱBD=2��10=20��cm����
�����������
��R��Q�ĺ���ʱ����ͼ1�� ��BR=BD+DR=20+3��t-12��=3t-16��
��BR=BD+DR=20+3��t-12��=3t-16��
��RQ=BQ-BR=2t-��3t-16��=16-t��
PE=BE-BP=$\frac{1}{2}$��2t-12=t-12��
��RQ=$\frac{1}{2}$PE��
��16-t=$\frac{1}{2}$��t-12����
���t=$\frac{44}{3}$��
��R��Q��ǰ��ʱ����ͼ2��
��BR=BD+DR=20+3��t-12��=3t-16��
��RQ=BR-BQ=3t-16-2t=t-16��
PE=BE-BP=$\frac{1}{2}$��2t-12=t-12��
��RQ=$\frac{1}{2}$PE��
��t-16=$\frac{1}{2}$��t-12����
���t=20��
�ʵ�tΪ$\frac{44}{3}$s��20sʱ��RQ=$\frac{1}{2}$PE��
���� ���⿼����һԪһ�η��̵�Ӧ�ã������ľ��룬·�̡��ٶ���ʱ��֮��Ĺ�ϵ������ؼ���Ҫ������Ŀ����˼��������Ŀ�������������ҳ����ʵĵ�����ϵ�г����̣�����⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | -3x | B�� | 3x | C�� | -6x | D�� | 3x5 |
| A�� | ��kֵ�ı仯���仯 | B�� | ����������ȵ�ʵ���� | ||
| C�� | ������ʵ���� | D�� | ��ʵ���� |
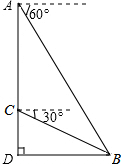 �����ԭ�ϣ���̫��ÿ�춼�������ץ�������Ű����ԣ���������������ͼ��ʾ��һ�죬��̫�����ԼҳDZ�����A��������������ڵ�B���ĸ���Ϊ60�㣬Ȼ���µ��DZ���C�������B���ĸ���Ϊ30�㣮��֪AC=50�ף���ʱ��������뱤�ײ�D�ж�Զ��
�����ԭ�ϣ���̫��ÿ�춼�������ץ�������Ű����ԣ���������������ͼ��ʾ��һ�죬��̫�����ԼҳDZ�����A��������������ڵ�B���ĸ���Ϊ60�㣬Ȼ���µ��DZ���C�������B���ĸ���Ϊ30�㣮��֪AC=50�ף���ʱ��������뱤�ײ�D�ж�Զ��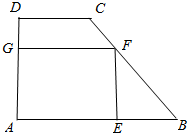 ��ͼ����һ����������ABCD��AB��CD����A=90�㣬AB=6cm��CD=2cm��AD=4cm�����������м���һ�ڽӾ�������AEFG������E��AB�ϣ�F��BC�ϣ�G��AD�ϣ����������Ϊ9cm2������ε�һ��EF��Ϊ���٣�
��ͼ����һ����������ABCD��AB��CD����A=90�㣬AB=6cm��CD=2cm��AD=4cm�����������м���һ�ڽӾ�������AEFG������E��AB�ϣ�F��BC�ϣ�G��AD�ϣ����������Ϊ9cm2������ε�һ��EF��Ϊ���٣�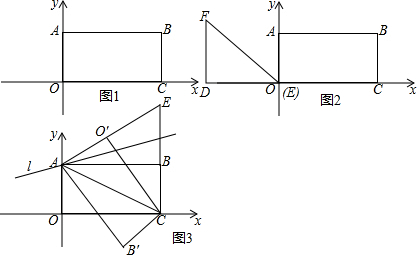
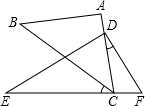 ��һ��ֱ�����ǰ���ͼ�ڷţ���C��EF�ϣ�AC������D����A=��EDF=90�㣬��BCE=40�㣬���CDF=25�㣮
��һ��ֱ�����ǰ���ͼ�ڷţ���C��EF�ϣ�AC������D����A=��EDF=90�㣬��BCE=40�㣬���CDF=25�㣮