题目内容
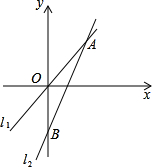 如图,已知:A(3,4),|OB|=2|OA|,求出直线l1和l2的解析式.
如图,已知:A(3,4),|OB|=2|OA|,求出直线l1和l2的解析式.考点:两条直线相交或平行问题
专题:
分析:先用待定系数法求出直线l1的解析式,再根据2OA=OB可求出B的坐标,把A,B两点代入直线l2的解析式即可.
解答:
解:设直线l1的解析式为y=k1x,
3k1=4,k1=
,即直线l1的解析式为:y=
x,
∵A(3,4)
∴OA=5,
∵OB=2OA,
∴OB=10,
∴B(0,-10),
设直线l2的解析式为y=k2x+b.则有:
,
∴k2=
,
即直线l2的解析式为:y=
x-10.
3k1=4,k1=
| 4 |
| 3 |
| 4 |
| 3 |
∵A(3,4)
∴OA=5,
∵OB=2OA,
∴OB=10,
∴B(0,-10),
设直线l2的解析式为y=k2x+b.则有:
|
∴k2=
| 14 |
| 3 |
即直线l2的解析式为:y=
| 14 |
| 3 |
点评:本题考查了两条直线相交或平行问题,要注意利用一次函数的特点,列出方程,求出未知数,再根据一次函数图象的特点解答,需同学们熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列方程变形错误的是( )
A、由方程
| ||||
B、由方程
| ||||
C、由方程
| ||||
D、由方程x-
|
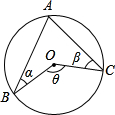 如图,AB,AC是O的两条弦,圆心O在∠BAC的内部,若∠ABO=α,∠ACO=β,∠BOC=θ,则下列关系式中,正确的是( )
如图,AB,AC是O的两条弦,圆心O在∠BAC的内部,若∠ABO=α,∠ACO=β,∠BOC=θ,则下列关系式中,正确的是( )| A、θ=α+β |
| B、θ+α+β=360° |
| C、θ+α+β=180° |
| D、θ=2α+2β |
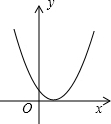 二次函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c-3=0的根的情况是( )
二次函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c-3=0的根的情况是( )| A、有两个不相等的实数根 |
| B、有两个异号实数根 |
| C、有两个相等的实数 |
| D、无实数根 |
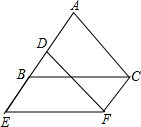 如图,△DEF是由△ABC沿AB方向平移2cm得到的,已知△ABC的周长为22cm,则四边形AEFC的周长为( )
如图,△DEF是由△ABC沿AB方向平移2cm得到的,已知△ABC的周长为22cm,则四边形AEFC的周长为( )| A、22cm | B、24cm |
| C、26cm | D、28cm |
 等边△ABC中,D在AB上,E在BC延长线上,AD=CE,DE交AC于G.求证:点G是DE中点.
等边△ABC中,D在AB上,E在BC延长线上,AD=CE,DE交AC于G.求证:点G是DE中点.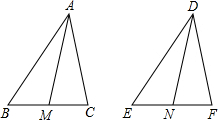
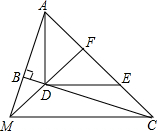 如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD⊥DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD⊥DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.