题目内容
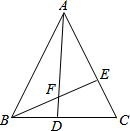 边长为4的等边△ABC,D,E分别在BC,AC上移动,D点从B运动到C,E从C运动到A.已知:D,E同时同速移动,连AD、BE交于F.
边长为4的等边△ABC,D,E分别在BC,AC上移动,D点从B运动到C,E从C运动到A.已知:D,E同时同速移动,连AD、BE交于F.(1)D、E在运动过程中,∠AFE是否发生变化?若不变,求∠AFE度数;若改变,说明理由.
(2)当△AFE为Rt△时,D、E分别在BC、AC的什么位置,并求EF长.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据∠BFD=∠ABE+∠BAD,∠ABE=∠CAD,可知∠BFD=∠CAD+∠BAD=∠BAC=60°=∠AFE;
(2)当△AFE为Rt△时,可得D、E分别在BC、AC的中点位置.
(2)当△AFE为Rt△时,可得D、E分别在BC、AC的中点位置.
解答:
(1)解:不变化,是60°,理由如下:
∵△ABC为等边三角形,
∴∠BAC=∠C=60°,AB=CA.
在△ABE与△CAD中,
,
∴△ABE≌△CAD(SAS).
∴∠ABE=∠CAD.
∵∠BFD=∠ABE+∠BAD,
∴∠BFD=∠CAD+∠BAD=∠BAC=60°
∴∠AFE=∠BFD=60°
 (2)当△AFE为Rt△时,D、E分别在BC、AC的中点,
(2)当△AFE为Rt△时,D、E分别在BC、AC的中点,
连接CF,
在Rt△CFE中,CE=
AC=2,∠FCE=30°,
设EF为x,则CF=2x,根据勾股定理可得:
x2+22=(2x)2
解得:x=
∴EF=
∵△ABC为等边三角形,
∴∠BAC=∠C=60°,AB=CA.
在△ABE与△CAD中,
|
∴△ABE≌△CAD(SAS).
∴∠ABE=∠CAD.
∵∠BFD=∠ABE+∠BAD,
∴∠BFD=∠CAD+∠BAD=∠BAC=60°
∴∠AFE=∠BFD=60°
 (2)当△AFE为Rt△时,D、E分别在BC、AC的中点,
(2)当△AFE为Rt△时,D、E分别在BC、AC的中点,连接CF,
在Rt△CFE中,CE=
| 1 |
| 2 |
设EF为x,则CF=2x,根据勾股定理可得:
x2+22=(2x)2
解得:x=
2
| ||
| 3 |
∴EF=
2
| ||
| 3 |
点评:本题考查三角形全等的性质和判定方法以及等边三角形的性质.判定两个三角形全等的一般方法有:SSS、SAS、AAS、ASA、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
如图所示,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②∠A=∠D;∠B=∠E,∠C=∠F;③AB=DE,BC=EF,∠B=∠E;④AB=DE,∠C=∠F,AC=DF.其中能使△ABC≌△DEF的条件的组数共有( )
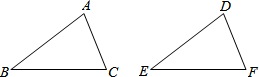

| A、1组 | B、2组 | C、3组 | D、4组 |
若a、b互为相反数,c、d互为倒数,|m|=2,则代数式m2-3cd+
的值为( )
| a+b |
| m |
| A、-1 | B、1 | C、-7 | D、1或-7 |
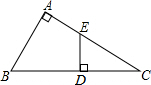 如图,已知∠A=90°,AB=BD,ED⊥BC于D.求证:AE=ED.
如图,已知∠A=90°,AB=BD,ED⊥BC于D.求证:AE=ED.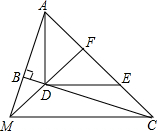 如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD⊥DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD⊥DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.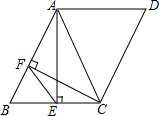 已知如图,在?ABCD中,∠D=60°,AE⊥BC,CF⊥AB,垂足分别为E,F.求证:AC=2EF.
已知如图,在?ABCD中,∠D=60°,AE⊥BC,CF⊥AB,垂足分别为E,F.求证:AC=2EF.