题目内容
二次函数y=x2-2x+m与x轴有交点,则m应满足的条件是( )
| A、m>1 | B、m≥1 |
| C、m<1 | D、m≤1 |
考点:抛物线与x轴的交点
专题:
分析:令y=0可得到关于x的一元二次方程,再利用一元二次方程根的判别式可得到关于m的不等式,可求得m满足的条件.
解答:
解:令y=0,可得x2-2x+m=0,
∵二次函数y=x2-2x+m与x轴有交点,
∴方程x2-2x+m=0有实数根,
∴△≥0,即4-4m≥0,
解得m≤1.
故选D.
∵二次函数y=x2-2x+m与x轴有交点,
∴方程x2-2x+m=0有实数根,
∴△≥0,即4-4m≥0,
解得m≤1.
故选D.
点评:本题主要考查二次函数与方程的关系,掌握二次函数图象与x轴的交点横坐标是对应一元二次方程的根是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
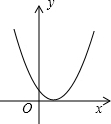 二次函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c-3=0的根的情况是( )
二次函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c-3=0的根的情况是( )| A、有两个不相等的实数根 |
| B、有两个异号实数根 |
| C、有两个相等的实数 |
| D、无实数根 |
一个角的平分线与该角的邻补角的平分线的夹角为( )
| A、80° | B、90° |
| C、45° | D、180° |
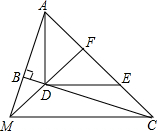 如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD⊥DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD⊥DE,点F是AE的中点,FD与AB的延长线相交于点M,连结MC.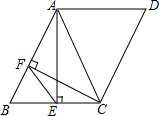 已知如图,在?ABCD中,∠D=60°,AE⊥BC,CF⊥AB,垂足分别为E,F.求证:AC=2EF.
已知如图,在?ABCD中,∠D=60°,AE⊥BC,CF⊥AB,垂足分别为E,F.求证:AC=2EF.