题目内容
1. 如图,在Rt△ABC中,∠C=90°,AD是BC边上的中线,BD=$\sqrt{2}$,∠B=30°,求AD的长.
如图,在Rt△ABC中,∠C=90°,AD是BC边上的中线,BD=$\sqrt{2}$,∠B=30°,求AD的长.
分析 根据线段中点的定义得到BC=2BD=2CD=2$\sqrt{2}$,由三角函数的定义得到AC=BC•tan30°=$\frac{2\sqrt{6}}{3}$,由勾股定理即可得到AD=$\sqrt{C{D}^{2}+A{C}^{2}}$=$\frac{4\sqrt{6}}{3}$.
解答 解:∵AD是BC边上的中线,BD=$\sqrt{2}$,
∴BC=2BD=2CD=2$\sqrt{2}$,
∵∠C=90°,∠B=30°,
∴AC=BC•tan30°=$\frac{2\sqrt{6}}{3}$,
∴AD=$\sqrt{C{D}^{2}+A{C}^{2}}$=$\frac{\sqrt{42}}{3}$.
点评 本题考查了勾股定理,含30°角的直角三角形的性质,三角函数的定义,得出BC=2BD=2CD是解题的关键.

练习册系列答案
相关题目
 已知,A、B两艘军舰同时从一港口出发,A的速度为20kn,B的速度为15kn,B一直向东航行,而A先向南航行30n mile后要按北偏东方向航行与B会合,求从出发开始多少时间A、B可以会合?
已知,A、B两艘军舰同时从一港口出发,A的速度为20kn,B的速度为15kn,B一直向东航行,而A先向南航行30n mile后要按北偏东方向航行与B会合,求从出发开始多少时间A、B可以会合? 如图,a⊥b,c与b不垂直.求证:a与c必相交.
如图,a⊥b,c与b不垂直.求证:a与c必相交.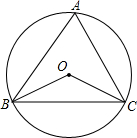 如图.点O是△ABC的外心.∠A=72°.
如图.点O是△ABC的外心.∠A=72°.
 如图表示一个由相同小立块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,画出这个几何体的左视图和主视图.
如图表示一个由相同小立块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,画出这个几何体的左视图和主视图. 如图,能用字母表示出的线段,射线和直线分别有哪几条?
如图,能用字母表示出的线段,射线和直线分别有哪几条?