题目内容
6．如图，下列正多边形分别是正三角形、正方形、正五边形、正六边形，已知正n边形的内角和为（n-2）180°．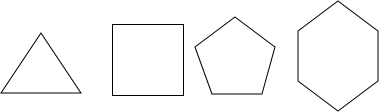
（1）正三角形的每个内角为60°；
（2）正方形的每个内角为90°；
（3）正五边形的每个内角为108°；
（4）正六边形的每个内角为120°；
（5）正n边形的每个内角为$\frac{（n-2）×18{0}^{°}}{n}$．
分析 （1）先计算出三角形的内角和，再除以3，即可解答；
（2）先计算出正方形形的内角和，再除以4，即可解答；
（3）先计算出正五边形形的内角和，再除以5，即可解答；
（4）先计算出正六边形的内角和，再除以6，即可解答；
（5）先计算出正n边形形的内角和，再除以n，即可解答；
解答 解：（1）正三角形的每个内角为：180°÷3=60°，故答案为：60°；
（2）正方形的每个内角为：360°÷4=90°，故答案为：90°；
（3）正五边形的每个内角为：（5-2）×180°÷5=108°，故答案为：108°；
（4）正六边形的每个内角为：（6-2）×180°÷6=120°，故答案为：120°；
（5）正n边形的每个内角为：$\frac{（n-2）×18{0}^{°}}{n}$，故答案为：$\frac{（n-2）×18{0}^{°}}{n}$．
点评 本题考查了多边形的内角和，解决本题的关键是熟记多边形的内角和公式．
练习册系列答案
相关题目
在方格纸中，每个小方格的顶点称为格点，以格点连线为边的三角形叫做格点三角形．在如图所示的5×5方格中，已知点A（0，-2），B（-1，0），作格点△ABC，使它和△OAB相似（相似比不为1），求点C的坐标．
如图，直线AB．CD相交于点O，OE平分∠BOC，∠COF=90°．
如图，在Rt△ABC中，∠C=90°，AD是BC边上的中线，BD=$\sqrt{2}$，∠B=30°，求AD的长．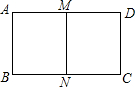
如图，在矩形ABCD中，AD＞AB，将其沿AD、BC的中点M，N对折后，得到的两个矩形与原矩形相似，求$\frac{AD}{AB}$的值．
设ab≠0且b＞a，