题目内容
9．
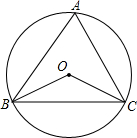如图．点O是△ABC的外心．∠A=72°．（1）求∠COB的度数．
（2）若BC=24cm．求△ABC外接圆的半径（精确到0.1cm）．
分析 （1）由圆周角定理即可得出结果；
（2）作OM⊥BC于M，则BM=CM=$\frac{1}{2}$BC=12cm，∠OMB=90°，∠BOM=$\frac{1}{2}$∠COB=72°，由三角函数求出OB即可．
解答 解：（1）∵点O是△ABC的外心．∠A=72°，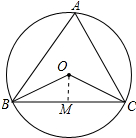
∴∠COB=2∠A=144°；
（2）作OM⊥BC于M，如图所示：
则BM=CM=$\frac{1}{2}$BC=12cm，∠OMB=90°，∠BOM=$\frac{1}{2}$∠COB=72°，
∵sin∠BOM=$\frac{BM}{OB}$，
∴OB=$\frac{BM}{sin72°}$=$\frac{12}{0.9511}$≈12.6（cm），
即△ABC外接圆的半径为12.6cm．
点评 本题考查了三角形的外接圆于外心、圆周角定理、垂径定理、等腰三角形的性质、三角函数；熟练掌握圆周角定理和垂径定理，运用三角函数求出OB是解决（2）的关键．
练习册系列答案
相关题目
如图，△ABC中，D为AB边上一点，已知AB=AC，AD=CD=BC，求△ABC中的各角的度数．
如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过D作⊙O的切线交AC于E，求证：DE⊥AC．
如图，直线AB．CD相交于点O，OE平分∠BOC，∠COF=90°．
二次函数y=$\frac{1}{2}$x2+2x-1的图象如图所示，利用该图象探索方程$\frac{1}{2}$x2+2x-1=0的正根的近似值（精确到0.1）．
如图，在Rt△ABC中，∠C=90°，AD是BC边上的中线，BD=$\sqrt{2}$，∠B=30°，求AD的长．
设ab≠0且b＞a，
19．
将一张正方形纸片剪成四个大小、形状一样的小正方形（如图所示），记为第一次操作，然后将其中的一片又按同样的方法剪成四小片，记为第二次操作，如此循环进行下去．请将下表中空缺的数据填写完整，并解答所提出的问题：
（1）如果剪100次，共能得到301个正方形．
（2）如果剪n次共能得到bn个正方形，试用含有n、bn的等式表示它们之间的数量关系．
bn=3n+1；
（3）若原正方形的边长为1，设an表示第n次所剪的正方形的边长，
①试用含n的式子表示an=an=（$\frac{1}{2}$）n．
②试猜想a1+a2+a3+a4+…+an-1+an与原正方形边长的数量关系，并用等式写出这个关系：1-（$\frac{1}{2}$）n．
（4）运用第（3）题的结论，求$\frac{2}{3}+\frac{5}{6}+\frac{11}{12}+\frac{23}{24}+\frac{47}{48}+\frac{95}{96}+\frac{191}{192}+\frac{383}{384}+\frac{767}{768}$的值．
将一张正方形纸片剪成四个大小、形状一样的小正方形（如图所示），记为第一次操作，然后将其中的一片又按同样的方法剪成四小片，记为第二次操作，如此循环进行下去．请将下表中空缺的数据填写完整，并解答所提出的问题：| 操作次数 | 1 | 2 | 3 | 4 | … |
| 正方形个数 | 4 | 7 | … |
（2）如果剪n次共能得到bn个正方形，试用含有n、bn的等式表示它们之间的数量关系．
bn=3n+1；
（3）若原正方形的边长为1，设an表示第n次所剪的正方形的边长，
①试用含n的式子表示an=an=（$\frac{1}{2}$）n．
②试猜想a1+a2+a3+a4+…+an-1+an与原正方形边长的数量关系，并用等式写出这个关系：1-（$\frac{1}{2}$）n．
（4）运用第（3）题的结论，求$\frac{2}{3}+\frac{5}{6}+\frac{11}{12}+\frac{23}{24}+\frac{47}{48}+\frac{95}{96}+\frac{191}{192}+\frac{383}{384}+\frac{767}{768}$的值．