题目内容
 已知,如图,Rt△ABC中,∠ABC=90°.
已知,如图,Rt△ABC中,∠ABC=90°.(1)利用直尺和圆规按要求完成作图(保留作图痕迹);
①作线段AC的垂直平分线,交AC于点M;
②连接BM,在BM的延长线上取一点D,使MD=MB,连接AD、CD.
(2)试判断(1)中四边形ABCD的形状,并说明理由.
考点:作图—复杂作图,矩形的判定
专题:
分析:(1)①利用线段垂直平分线的作法得出即可;
②利用射线的作法得出D点位置;
(2)利用直角三角形斜边与其边上中线的关系进而得出AM=MC=BM=DM,进而得出答案.
②利用射线的作法得出D点位置;
(2)利用直角三角形斜边与其边上中线的关系进而得出AM=MC=BM=DM,进而得出答案.
解答: 解:(1)①如图所示:M点即为所求;
解:(1)①如图所示:M点即为所求;
②如图所示:四边形ABCD即为所求;
(2)矩形,
理由:∵Rt△ABC中,∠ABC=90°,BM是AC边上的中线,
∴BM=
AC,
∵BM=DM,AM=MC
∴AM=MC=BM=DM,
∴四边形ABCD是矩形.
 解:(1)①如图所示:M点即为所求;
解:(1)①如图所示:M点即为所求;②如图所示:四边形ABCD即为所求;
(2)矩形,
理由:∵Rt△ABC中,∠ABC=90°,BM是AC边上的中线,
∴BM=
| 1 |
| 2 |
∵BM=DM,AM=MC
∴AM=MC=BM=DM,
∴四边形ABCD是矩形.
点评:此题主要考查了复杂作图以及矩形的判定,得出BM=
AC是解题关键.
| 1 |
| 2 |

练习册系列答案
相关题目
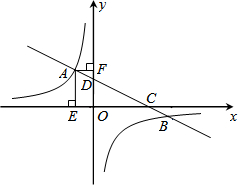 如图,一次函数y=ax+b与反比例函数
如图,一次函数y=ax+b与反比例函数 如图,PA,PB分别与⊙O相切于点A,B,∠APB=60°,连接AO,BO.
如图,PA,PB分别与⊙O相切于点A,B,∠APB=60°,连接AO,BO.
