题目内容
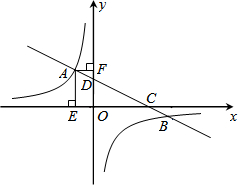 如图,一次函数y=ax+b与反比例函数y=-
如图,一次函数y=ax+b与反比例函数y=-| 2 |
| x |
(1)请直接写出矩形AEOF的面积;
(2)设一次函数y=ax+b与x轴、y轴的交点分别为C、D,当OC=3OE时.
①试求△OCD的面积;
②当OE=1时,以BD为直径作⊙N,与x轴相交于P点,请求出P点的坐标.
考点:反比例函数综合题,待定系数法求一次函数解析式,反比例函数系数k的几何意义,勾股定理,垂径定理,相似三角形的判定与性质
专题:综合题
分析:(1)由反比例函数系数k的几何意义即可得到矩形AEOF的面积.
(2)①设OE=m(m>0),即可用m表示出点A、C的坐标,再由△DOC∽△AEC即可求出OD的长度(用m表示),进而可以求出△DOC的面积.
②由OE=1得m=1,从而得到点A、C的坐标,进而求出直线AC的解析式,就可求出点D、B的坐标,以及BD的长度(即⊙N的直径),然后借助于三角形相似就可求出点N的坐标,再借助于勾股定理即可求出点P的坐标.
(2)①设OE=m(m>0),即可用m表示出点A、C的坐标,再由△DOC∽△AEC即可求出OD的长度(用m表示),进而可以求出△DOC的面积.
②由OE=1得m=1,从而得到点A、C的坐标,进而求出直线AC的解析式,就可求出点D、B的坐标,以及BD的长度(即⊙N的直径),然后借助于三角形相似就可求出点N的坐标,再借助于勾股定理即可求出点P的坐标.
解答:解:(1)如图1,
∵点A在反比例函数y=-
的图象上,
且AE⊥x轴,AF⊥y轴,
∴S矩形AEOF=
=2.
∴矩形AEOF的面积为2.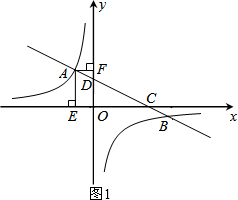
(2)①如图1,
设OE=m(m>0),则E(-m,0).
∴C(3m,0),A(-m,
).
∴OC=3m,CE=4m,AE=
.
∵AE⊥x轴、AF⊥y轴,
∴∠DOC=∠AEC=90°.
又∵∠DCO=∠ACE,
∴△DOC∽△AEC.
∴
=
.
∴
=
.
∴OD=
.
∴S△OCD=
OC•DO=
×3m×
=
.
∴△OCD的面积为
.
②过点N作NG⊥y轴,垂足为G,过点B作BH⊥y轴,垂足为H,过点N作NM⊥x轴,垂足为M,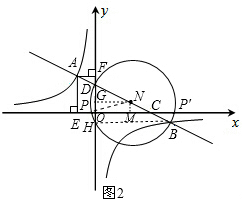 连接NP,如图2所示.
连接NP,如图2所示.
∵OE=1,
∴m=1.
∴A(-1,2),C(3,0).
∵点A、点C在直线y=ax+b上,
∴
解得:
.
∴y=-
x+
.
当x=0时,y=
.
∴OD=
.
∵A、B是直线y=-
x+
与反比例函数y=-
图象的交点,
∴-
x+
=-
.
解得:x1=-1,x2=4.
当x1=-1时,y1=2;
当x2=4时,y2=-
.
∴点B的坐标为(4,-
).
∴BH=4,OH=
.
∴DH=2.
∵∠BHD=90°,
∴BD=
=
=2
.
∴PN=
.
∵NG⊥y轴,BH⊥y轴
∴NG∥BH
∴△DGN∽△DHB.
∴
=
=
.
∵DN=
DB,
∴DG=
DH,NG=
BH=2.
∵点N在直线y=-
x+
上,
∴点N(2,
).
∴NM=
.
∵NM⊥PP′,
∴PM=P′M,∠NMP=90°.
∵PN=
,NM=
,
∴PM2=NP2-MN2=
.
∴PM=
.
∴P′M=
.
∴P点的坐标为(2-
,0)或(
+2,0).
∵点A在反比例函数y=-
| 2 |
| x |
且AE⊥x轴,AF⊥y轴,
∴S矩形AEOF=
|
∴矩形AEOF的面积为2.

(2)①如图1,
设OE=m(m>0),则E(-m,0).
∴C(3m,0),A(-m,
| 2 |
| m |
∴OC=3m,CE=4m,AE=
| 2 |
| m |
∵AE⊥x轴、AF⊥y轴,
∴∠DOC=∠AEC=90°.
又∵∠DCO=∠ACE,
∴△DOC∽△AEC.
∴
| OD |
| AE |
| OC |
| CE |
∴
| OD | ||
|
| 3m |
| 4m |
∴OD=
| 3 |
| 2m |
∴S△OCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2m |
| 9 |
| 4 |
∴△OCD的面积为
| 9 |
| 4 |
②过点N作NG⊥y轴,垂足为G,过点B作BH⊥y轴,垂足为H,过点N作NM⊥x轴,垂足为M,
 连接NP,如图2所示.
连接NP,如图2所示.∵OE=1,
∴m=1.
∴A(-1,2),C(3,0).
∵点A、点C在直线y=ax+b上,
∴
|
解得:
|
∴y=-
| 1 |
| 2 |
| 3 |
| 2 |
当x=0时,y=
| 3 |
| 2 |
∴OD=
| 3 |
| 2 |
∵A、B是直线y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| x |
∴-
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| x |
解得:x1=-1,x2=4.
当x1=-1时,y1=2;
当x2=4时,y2=-
| 1 |
| 2 |
∴点B的坐标为(4,-
| 1 |
| 2 |
∴BH=4,OH=
| 1 |
| 2 |
∴DH=2.
∵∠BHD=90°,
∴BD=
| DH2+BH2 |
| 22+42 |
| 5 |
∴PN=
| 5 |
∵NG⊥y轴,BH⊥y轴
∴NG∥BH
∴△DGN∽△DHB.
∴
| DG |
| DH |
| GN |
| HB |
| DN |
| DB |
∵DN=
| 1 |
| 2 |
∴DG=
| 1 |
| 2 |
| 1 |
| 2 |
∵点N在直线y=-
| 1 |
| 2 |
| 3 |
| 2 |
∴点N(2,
| 1 |
| 2 |
∴NM=
| 1 |
| 2 |
∵NM⊥PP′,
∴PM=P′M,∠NMP=90°.
∵PN=
| 5 |
| 1 |
| 2 |
∴PM2=NP2-MN2=
| 19 |
| 4 |
∴PM=
| ||
| 2 |
∴P′M=
| ||
| 2 |
∴P点的坐标为(2-
| ||
| 2 |
| ||
| 2 |
点评:本题考查了反比例函数系数的几何意义、相似三角形的判定与性质、勾股定理、垂径定理、用待定系数法求一次函数的解析式等知识,有一定的综合性.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
某商品原价5元,如果跌价x%后,仍不低于4元,那么( )
| A、x≤20 | B、x<20 |
| C、x≥20 | D、x>20 |
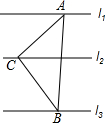 如图,已知△ABC中,∠ACB=90°,AC=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2与l3之间的距离为3,则△ABC的面积是
如图,已知△ABC中,∠ACB=90°,AC=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2与l3之间的距离为3,则△ABC的面积是

 已知,如图,Rt△ABC中,∠ABC=90°.
已知,如图,Rt△ABC中,∠ABC=90°.