题目内容
某校为了解学生对三种国庆活动方案的意见,对该校学生进行了一次抽样调查(被调查学生至多赞成其中的一种方案),现将调查结果绘制成如图两幅不完整的统计图.

请根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了 名学生;扇形统计图中方案1所对应的圆心角的度数为 度;
(2)请把条形统计图补充完整;
(3)已知该校有1000名学生,试估计该校赞成方案1的学生约有多少人?

请根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了
(2)请把条形统计图补充完整;
(3)已知该校有1000名学生,试估计该校赞成方案1的学生约有多少人?
考点:条形统计图,用样本估计总体,扇形统计图
专题:
分析:(1)根据赞成方案3的有15人,占25%,据此即可求得调查的总人数,利用360°乘以对应的比例即可求得图中方案1所对应的圆心角的度数;
(2)利用总人数减去其它各组的人数,即可求得赞成方案2的人数,从而作出直方图;
(3)利用总人数1000乘以对应的比例即可求解.
(2)利用总人数减去其它各组的人数,即可求得赞成方案2的人数,从而作出直方图;
(3)利用总人数1000乘以对应的比例即可求解.
解答:解:(1)调查的总人数是:15÷25%=60(人),
扇形统计图中方案1所对应的圆心角的度数是:360°×
=144°;
(2)赞成方案2的人数是:60-24-15-9=12(人),
 ;
;
(3)该校赞成方案1的学生约有:1000×
=400(人).
扇形统计图中方案1所对应的圆心角的度数是:360°×
| 24 |
| 60 |
(2)赞成方案2的人数是:60-24-15-9=12(人),
 ;
;(3)该校赞成方案1的学生约有:1000×
| 24 |
| 60 |
点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
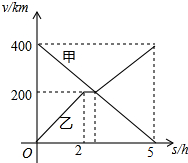 甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题: 已知,如图,Rt△ABC中,∠ABC=90°.
已知,如图,Rt△ABC中,∠ABC=90°. 如图,已知∠DAB=70°,AC平分∠DAB,∠1=35°,求∠D的度数.
如图,已知∠DAB=70°,AC平分∠DAB,∠1=35°,求∠D的度数.