题目内容
7. 已知点A、B在数轴的位置如图:
已知点A、B在数轴的位置如图:(1)若点P在数轴上,且PA+PB=6,求点P对应的数;
(2)若点M在数轴上,MA:MB=1:3,求点M对应的数.
分析 (1)根据题意可得符合要求的点P有两个,然后讨论可得点P对应的数;
(2)根据题意可得符合要求的点M有两个,然后讨论可得点M对应的数.
解答 解:(1)根据题意可知,符合要求的点P有两种情况,
当点P在点A右侧时,设点P表示的数是a,
则(a-1)+[a-(-3)]=6
解得,a=2;
当点P在点B的左侧时,设点P表示的数是b,
则(1-b)+[(-3)-b]=6
解得,b=-4;
即点P对应的数是2或-4.
(2)根据题意可知,符合要求的点M有两种情况,
当点M在点A的右侧时,设点M表示的数是c,
(c-1):[c-(-3)]=1:3
解得,c=3;
当点M在点A与B之间时,设点M表示的数是d,
(1-d):[d-(-3)]=1:3
解得,d=0.
即点M表示的数是3或0.
点评 本题考查数轴,解题的关键是利用分类讨论的数学思想解答问题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
18.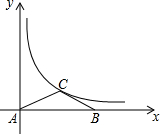 如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
 如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )| A. | 一直不变 | B. | 先增大后减小 | C. | 先减小后增大 | D. | 先增大后不变 |
15.估算$\sqrt{29}$-2的值( )
| A. | 在1至2之间 | B. | 在2至3之间 | C. | 在3至4之间 | D. | 在4至5之间 |