题目内容
17.直线y=4x-2与直线y=-x+13及x轴所围成的三角形的面积为$\frac{125}{2}$.分析 先求出两直线与x轴交点的坐标,以及两条直线的交点坐标,然后再根据三角形的面积公式求出所围三角形的面积.
解答 解:直线y=4x-2与x轴的交点坐标是($\frac{1}{2}$,0),
直线y=-x+13与x轴的交点坐标是(13,0),
由$\left\{\begin{array}{l}{y=4x-2}\\{y=-x+13}\end{array}\right.$得直线y=4x-2与直线y=-x+13的交点坐标是(3,10),
如图:
直线y=4x-2与直线y=-x+13与x轴围成的三角形的面积为$\frac{1}{2}$×$\frac{25}{2}$×10=$\frac{125}{2}$.
故答案为:$\frac{125}{2}$.
点评 此题考查了两条直线相交与平行问题,关键是通过求出两直线的交点和与x轴的交点求出三角形的边长和高,用到的知识点是求两直线的交点、三角形的面积公式.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
 已知点A、B在数轴的位置如图:
已知点A、B在数轴的位置如图: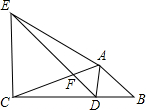 如图,在△ABC中,将△ABC绕点A顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上,且DE∥AB交AC于F时.
如图,在△ABC中,将△ABC绕点A顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上,且DE∥AB交AC于F时. 在平面直角坐标系xOy中,直线y=-2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=-2x+1交于点B,设点B的横坐标为x0.
在平面直角坐标系xOy中,直线y=-2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=-2x+1交于点B,设点B的横坐标为x0.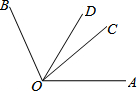 如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=23°,求∠AOB的度数.
如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=23°,求∠AOB的度数.