题目内容
2.在△ABC中,已知AC=5,且$\frac{1}{tan\frac{A}{2}}$+$\frac{1}{tan\frac{C}{2}}$-$\frac{5}{tan\frac{B}{2}}$=0,则BC+AB=( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 做出三角形的三个内角的平分线,相交于O,过O作三边的垂线,最后用三角函数即可.
解答 解:如图:
作∠ABC,∠BCA,∠CAB的平分线相交于点O,过O作OD⊥BC,OE⊥AC,OF⊥AB,
设AF=m,BF=n,OD=OE=OF=r,
∴AE=m.BD=n,
∵AC=5,
∴CE=CD=5-m,
在Rt△AOF中,tan∠BAO=$\frac{r}{m}$,
∴$\frac{1}{tan∠BAO}=\frac{m}{r}$,
同理:$\frac{5}{tan∠CBO}=\frac{5n}{r}$,
$\frac{1}{tan∠ACO}=\frac{5-m}{r}$,
∵$\frac{1}{tan\frac{A}{2}}$+$\frac{1}{tan\frac{C}{2}}$-$\frac{5}{tan\frac{B}{2}}$=0,
∴$\frac{m}{r}+\frac{5-m}{r}-\frac{5n}{r}$=0,
∴n=1,
∴AB+BC=m+n+n+5-m=2n+5=7,
故选B
点评 此题是解直角三角形,主要考查了三角形的角平分线的意义,三角函数,解本题的关键是构造直角三角形.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
7.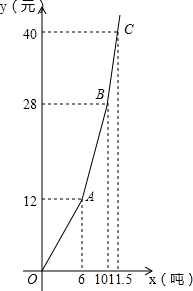 为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).
为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).
(1)填空
价目表
(2)若某户居民9月份用水量为9.5吨,求该用户9月份水费;
(3)若某户居民10月份水费30元,求该用户10月份用水量;
(4)若某户居民11月、12月共用水18吨,其中11月用水a(吨),用含a的代数式表示该户居民11月、12月共应交水费Q(元).
 为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).
为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).(1)填空
价目表
| 每月水用量 | 单价 |
| 不超出6吨的部分 | 2元/吨 |
| 超出6吨不超出10吨的部分 | 4 元/吨 |
| 超出10吨的部分 | 8元/吨 |
(3)若某户居民10月份水费30元,求该用户10月份用水量;
(4)若某户居民11月、12月共用水18吨,其中11月用水a(吨),用含a的代数式表示该户居民11月、12月共应交水费Q(元).
11.下列命题中,是真命题的是( )
| A. | 有理数都是有限小数 | |
| B. | 同旁内角互补 | |
| C. | 函数y=$\frac{1}{\sqrt{x-3}}$自变量x的取值范围是x≥3 | |
| D. | 若甲、乙两组数据中各有20个数据,平均数$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,方差S甲2=1.25,S乙2=0.96,则说明乙组数据比甲组数据稳定 |
12. 在下列软件的图标中,其中是中心对称图形的有( )
在下列软件的图标中,其中是中心对称图形的有( )
 在下列软件的图标中,其中是中心对称图形的有( )
在下列软件的图标中,其中是中心对称图形的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |