题目内容
12. 如图,已知△ABC,AB=AC,∠A=36°
如图,已知△ABC,AB=AC,∠A=36°①用尺规作线段AB的垂直平分线,垂足为M,交AC于N(不写作法,保留作图痕迹)
②求证:△BNC是等腰三角形.
分析 ①根据要求画出线段AB的垂直平分线即可;
②只要证明∠BNC=∠C=72°即可.
解答 解:①如图直线MN即为所求.
②连接BN.
∵MN是AB的垂直平分线,
∴NA=NB,
∴∠A=∠NBA=36°,
∴∠BNC=∠A+∠BNA=72°,
∵AB=AC,∠A=36°,
∴∠C=∠ABC=$\frac{1}{2}$(180°-36°)=72°,
∴∠C=∠CNB,
∴BN=BC,
∴△BNC是等腰三角形.
点评 本题考查等腰三角形的性质,线段的垂直平分线等知识,解题的关键是熟练掌握五种基本作图,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
2.某种禽流感病毒变异后的直径为0.00000018米,0.00000018米用科学记数法表示为( )
| A. | 1.8×10-5米 | B. | 0.18×10-6米 | C. | 1.8×10-7米 | D. | 18×10-8米 |
17.下面四个多项式中,能进行因式分解的是( )
| A. | x2+y2 | B. | x2-y | C. | x2-1 | D. | x2+x+1 |
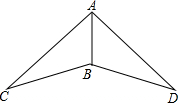 如图,△ABC与△ABD中,BC=BD,AE、AF分别是∠BAC、∠BAD的角平分线.
如图,△ABC与△ABD中,BC=BD,AE、AF分别是∠BAC、∠BAD的角平分线.