题目内容
6.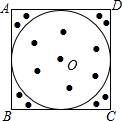 正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )
正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )| A. | π≈$\frac{a}{b}$ | B. | π≈$\frac{4b}{a}$ | C. | π≈$\frac{b}{a}$ | D. | π≈$\frac{4a}{b}$ |
分析 根据圆的面积与正方形的面积的比等于落在相应位置的点数的比列式求解即可.
解答 解:设圆的半径为r,则正方形的边长为2r,
根据题意得:$\frac{π{r}^{2}}{4{r}^{2}}$≈$\frac{b}{a}$,
故π≈$\frac{4b}{a}$,
故选B.
点评 本题考查了利用频率估计概率的知识,解题的关键是能够了解落在圆内的概率约等于圆与正方形的面积的比,难度不大.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
16. 如图,在⊙O中,∠AOB=50°,则∠ACB=( )
如图,在⊙O中,∠AOB=50°,则∠ACB=( )
 如图,在⊙O中,∠AOB=50°,则∠ACB=( )
如图,在⊙O中,∠AOB=50°,则∠ACB=( )| A. | 30° | B. | 25° | C. | 50° | D. | 40° |
14.三角形的两边分别为5和6,第三边长是方程x2-6x+8=0的解,则这个三角形的周长是( )
| A. | 13 | B. | 15 | C. | 13或15 | D. | 13和15 |
18.用下列哪种方法解方程3(x-2)2=2x-4比较简便( )
| A. | 直接开平方法 | B. | 配方法 | C. | 公式法 | D. | 因式分解法 |
15.下列各式是完全平方式的是( )
| A. | x2+2x-1 | B. | 1+x2 | C. | x+xy+1 | D. | x2-2x+1 |
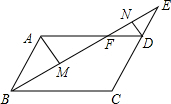 如图,在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.M,N分别是BF、EF的中点,若△DEF的面积为a,则AM:DN=2,则?ABCD的面积为12a.
如图,在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.M,N分别是BF、EF的中点,若△DEF的面积为a,则AM:DN=2,则?ABCD的面积为12a.