题目内容
5.分解因式:-3x+6x2-3x3=-3x(x-1)2.分析 首先提取公因式-3x,进而利用完全平方公式分解因式得出即可.
解答 解:-3x+6x2-3x3=-3x(1-2x+x2)=-3x(x-1)2.
故答案为:-3x(x-1)2.
点评 此题主要考查了提取公因式法以及公式法分解因式,熟练应用乘法公式是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.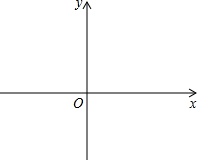 如图,在平面直角坐标系中,点P(m,n)是动点,且m、n的关系满足下表:
如图,在平面直角坐标系中,点P(m,n)是动点,且m、n的关系满足下表:
(1)①写出m、n的关系式n=-m+1;②再写出一组满足关系的m、n的值4,-3;
(2)将每一直列中m的值作为点的横坐标,n的值作为点的纵坐标,在同一平面直角坐标系中分别描出这些点,并用线顺次连接这些点,观察它是一个什么图形?
 如图,在平面直角坐标系中,点P(m,n)是动点,且m、n的关系满足下表:
如图,在平面直角坐标系中,点P(m,n)是动点,且m、n的关系满足下表:| m | … | -3 | -2 | 0 | 1 | 2 | 3 | … |
| n | … | 4 | 3 | 1 | 0 | -1 | -2 | … |
(2)将每一直列中m的值作为点的横坐标,n的值作为点的纵坐标,在同一平面直角坐标系中分别描出这些点,并用线顺次连接这些点,观察它是一个什么图形?
20.对于反比例函数$y=\frac{k}{x}$,如果当-2≤x≤-1时有最大值y=4,则当x≥8时,有( )
| A. | 最小值y=$-\frac{1}{2}$ | B. | 最小值y=-1 | C. | 最大值y=$-\frac{1}{2}$ | D. | 最大值y=-1 |
15.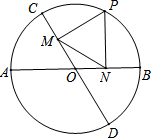 如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )
如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )
 如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )
如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )| A. | 随P点运动而变化,最大值为$\sqrt{3}$ | B. | 等于$\sqrt{3}$ | ||
| C. | 随P点运动而变化,最小值为$\sqrt{3}$ | D. | 随P点运动而变化,没有最值 |
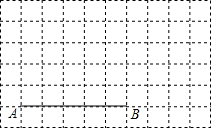 如图,在10×6的正方形网络中,每一个小正方形的边长均为1,线段AB的端点A、B均为在小正方形的顶点上.
如图,在10×6的正方形网络中,每一个小正方形的边长均为1,线段AB的端点A、B均为在小正方形的顶点上.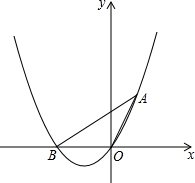 如图,一抛物线过原点和点A(1,$\sqrt{3}$),△AOB的面积为$\sqrt{3}$.
如图,一抛物线过原点和点A(1,$\sqrt{3}$),△AOB的面积为$\sqrt{3}$.