题目内容
13.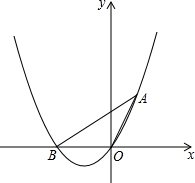 如图,一抛物线过原点和点A(1,$\sqrt{3}$),△AOB的面积为$\sqrt{3}$.
如图,一抛物线过原点和点A(1,$\sqrt{3}$),△AOB的面积为$\sqrt{3}$.(1)求过点A、O、B的抛物线解析式.
(2)在(1)中抛物线的对称轴上找到一点M,使△AOM的周长最小.
①点M的坐标是(-1,$\frac{\sqrt{3}}{3}$).
②求△AOM周长的最小值.
(3)点F为x轴上一动点,过点F作x轴的垂线,交直线AB于点E,交抛物线于点P,是否存在点F,使线段PE=$\frac{2\sqrt{3}}{3}$?若存在,直接写出点F的坐标;若不存在,请说明理由.
分析 (1)过A作AC⊥x轴于点C,由△AOB的面积可求得BO的长,可求得B点坐标,再利用待定系数法可求得抛物线解析式;
(2)①设AB于对称轴交于点M,则M点即为满足条件的点,可求得直线AB的解析式,可求得M坐标;②由勾股定理可求得AB、AO的长,则可求得△AOM的周长的最小值;
(3)可设F点坐标为(x,0),可表示出E、P的坐标,则可用x表示出PE的长,可求得x的值,可求出F的坐标.
解答 解:
(1)过A作AC⊥x轴于点C,如图1,
∵A(1,$\sqrt{3}$),
∴AC=$\sqrt{3}$,
∴$\frac{1}{2}$BO•AC=$\frac{1}{2}$BO×$\sqrt{3}$=$\sqrt{3}$,
∴BO=2,
∴B(-2,0),
由题意可设抛物线解析式为y=ax2+bx,
把A、B坐标代入可得$\left\{\begin{array}{l}{a+b=\sqrt{3}}\\{4a-2b=0}\end{array}\right.$,可解得$\left\{\begin{array}{l}{a=\frac{\sqrt{3}}{3}}\\{b=\frac{2\sqrt{3}}{3}}\end{array}\right.$,
∴过A、B、O三点的抛物线的解析式为y=$\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x;
(2)由(1)可求得抛物线的对称轴为x=-1,
设AB交对称轴于点M,如图2,
∵B、O关于对称轴对称,
∴MO=MB,
∴M点即为所求,
①设直线AB解析式为y=kx+b,
把A、B坐标代入可得$\left\{\begin{array}{l}{k+b=\sqrt{3}}\\{-2k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=\frac{2\sqrt{3}}{3}}\end{array}\right.$,
∴直线AB解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$,
当x=-1时,y=$\frac{\sqrt{3}}{3}$,
∴M坐标为(-1,$\frac{\sqrt{3}}{3}$),
故答案为:(-1,$\frac{\sqrt{3}}{3}$);
②由勾股定理可求得AB=$\sqrt{[1-(-2)]^{2}+(\sqrt{3})^{2}}$=2$\sqrt{3}$,AO=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∴△AOM周长的最小值为AM+MO+AO=AB+AO=2$\sqrt{3}$+2;
(3)假设存在满足条件的点F,设其坐标为(x,0),
则E(x,$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$),P(x,$\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x),如图3,
则PE=PF-EF=|($\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x)-($\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$)|=|$\frac{\sqrt{3}}{3}$x2+$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$|,
若PE=$\frac{2\sqrt{3}}{3}$,则|$\frac{\sqrt{3}}{3}$x2+$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$|=$\frac{2\sqrt{3}}{3}$,
当$\frac{\sqrt{3}}{3}$x2+$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$时,解得x=0或x=1,当x=0时,P点和F点重合,满足条件;
当x=1时,此时P、E重合,不满足条件,
∴此时F为(0,0),
∴存在满足条件的F点,其坐标为(0,0).
点评 本题主要考查二次函数的综合应用,涉及知识点有待定系数法求函数解析式、轴对称性质的应用、勾股定理和函数图象的交点等.在(1)中求得B点的坐标是解题的关键,在(2)中确定出M点的位置是解题的关键,在(3)中设出点F的坐标表示出PE的长是解题的关键.本题涉及知识点较多,综合性较强,难度较大.

 阅读快车系列答案
阅读快车系列答案32-12=8;
52-32=16;
72-52=24;
92-72=32;
…
根据上述规律,填空:132-112=48,192-172=72;
你能用含n的等式表示这一规律吗?你能说明它的正确性吗?
| A. | 买1根油条和1个大饼共2.5元 | B. | 2根油条比1个大饼便宜 | ||
| C. | 买2根油条和4个大饼共9元 | D. | 买5根油条和7个大饼共19元 |
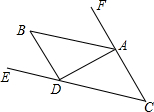 如图,已知AB∥CD,AB是∠FAD的平分线,∠C=45°.
如图,已知AB∥CD,AB是∠FAD的平分线,∠C=45°.