题目内容
10.写出以下命题的逆命题,判断逆命题的真假.若为假命题,请举反例;若为真命题,请给予证明.(1)一次函数y=kx+b,若k>0,b<0,则它的图象不经过第二象限;
(2)等腰三角形底边上的中点到两腰的距离相等.
分析 (1)把命题的题设与结论交换,再根据一次函数的图象的性质判断即可;
(2)把题设与结论交换,然后作出图形,根据中点性质可得BD=CD,利用“HL”证明Rt△BDE和Rt△CDF全等,根据全等三角形对应角相等可得∠B=∠C,再利用等角对等边证明AB=AC即可.
解答  解:(1)逆命题:一次函数y=kx+b,若它的图象不经过第二象限,则k>0,b<0,
解:(1)逆命题:一次函数y=kx+b,若它的图象不经过第二象限,则k>0,b<0,
是假命题,k>0,b=0也可以;
(2)逆命题,一边上的中点到其余两边的距离相等的三角形是等腰三角形;
已知:如图,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,
求证:三角形ABC为等腰三角形;
证明:如图,∵DE=DF,BD=CD,DE⊥AB,DF⊥AC
∴Rt△BDE≌Rt△CDF(HL),
∴∠B=∠C,
∴AB=AC(等角对等边)
∴△ABC为等腰三角形.
点评 本题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
18.买1根油条和3个大饼共7元,买3根油条和1个大饼共5元.下列说法中正确的是( )
| A. | 买1根油条和1个大饼共2.5元 | B. | 2根油条比1个大饼便宜 | ||
| C. | 买2根油条和4个大饼共9元 | D. | 买5根油条和7个大饼共19元 |

 如图,M、N是菱形ABCD的边BC、DC的中点,P是菱形的对角线BD上的动点,若BD=8,AC=6,求PM+PN的最小值.
如图,M、N是菱形ABCD的边BC、DC的中点,P是菱形的对角线BD上的动点,若BD=8,AC=6,求PM+PN的最小值.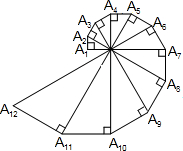 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为$\frac{1}{2}$×($\frac{2}{3}\sqrt{3}$)4026.
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为$\frac{1}{2}$×($\frac{2}{3}\sqrt{3}$)4026.