题目内容
15.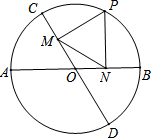 如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )
如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合).PM,PN分别垂直于CD,AB,垂足分别为M,N.若⊙O的半径长为2,则MN的长( )| A. | 随P点运动而变化,最大值为$\sqrt{3}$ | B. | 等于$\sqrt{3}$ | ||
| C. | 随P点运动而变化,最小值为$\sqrt{3}$ | D. | 随P点运动而变化,没有最值 |
分析 当PM⊥AB于圆心O时,延长PM交圆与点E,PN⊥CD,延长PN交圆于点F,连接EF,求出EF的长,得到MN的长,根据圆周角、圆心角、弧、弦之间的关系得到答案.
解答  解:如图,当PM⊥AB于圆心O时,延长PM交圆与点E,PN⊥CD,延长PN交圆于点F,连接EF,
解:如图,当PM⊥AB于圆心O时,延长PM交圆与点E,PN⊥CD,延长PN交圆于点F,连接EF,
根据垂径定理,MN=$\frac{1}{2}$EF,
∵∠AOD=120°,PM⊥AB,
∴∠PMN=30°,∠P=60°,
在Rt△PEF中,PE=4,则EF=2$\sqrt{3}$,
∴MN=$\sqrt{3}$,
点P移动时,由题意,∠P=60°,
根据在同圆中,圆周角相等,所对的弧相等,弦也相等,
即弦长为2$\sqrt{3}$,∴MN=$\sqrt{3}$,
故选:B.
点评 本题考查的是垂径定理、三角形中位线定理和锐角三角函数的运用,求出特殊情况下的MN的值是解题的关键,解答时,要灵活运用圆周角、圆心角、弧、弦之间的关系.

练习册系列答案
相关题目
6.一组数据:-1,1,3,4,a,若它们的平均数为2,则这组数据的众数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
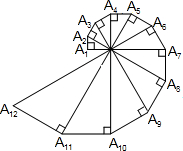 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为$\frac{1}{2}$×($\frac{2}{3}\sqrt{3}$)4026.
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为$\frac{1}{2}$×($\frac{2}{3}\sqrt{3}$)4026.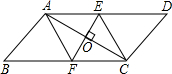 已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.求证:四边形AFCE是菱形.
已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.求证:四边形AFCE是菱形.