题目内容
20．
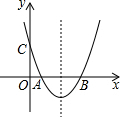如图，关于x的二次函数y=x2-x+m的图象交x轴的正半轴于A，B两点，交y轴的正半轴于C点，如果x=a时，y＜0，那么关于x的一次函数y=（a-1）x+m的图象可能是（ ）| A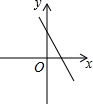． |  | B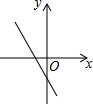． |  | C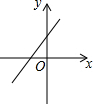． |  | D． |  |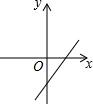
分析 根据函数图象与y轴的交点，可得m＞0，根据二次函数图象当x=a时，y＜0，可得a＞0，a-1＜0，根据一次函数的性质，可得答案．
解答 解：把x=a代入函数y=x2-x+m，得y=a2-a+m=a（a-1）+m，
∵x=a时，y＜0，即 a（a-1）+m＜0．
由图象交y轴的正半轴于点C，得m＞0，
即a（a-1）＜0．
x=a时，y＜0，∴a＞0，a-1＜0，
∴一次函数y=（a-1）x+m的图象过一二四象限，
故选：A．
点评 本题考查了二次函数图象，利用函数图象与y轴的交点得出m＞0，二次函数图象当x=a时，y＜0，得出a＞0，a-1＜0是解题关键．
练习册系列答案
相关题目
8．甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2；乙袋中装有3个完全相同的小球，分别标有数字-2，-1，0；从甲袋中随机抽取一个小球，再从乙袋中随机抽取一个小球，两球数字之和为1的概率是（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{2}{9}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{3}$ |
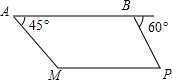如图，我巡逻机在海岛M上空巡逻，距离海平面垂直高度为1000米，在A点测得正前方海岛M的俯角为45°，在沿海面水平方向飞行2000米到达B点时测得一不明船只P的俯角为60°，已知A，B，P，M在同一水平面上，求不明船只P与海岛M之间的距离（结果保留根号）
5．计算（-ab2）3的结果是（ ）
| A． | a3b5 | B． | -a3b5 | C． | -a3b6 | D． | a3b6 |
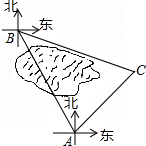五一期间，小明同学到滨湖湿地公园参加校无线电测向科技社团组织的实践活动，目标点B在观测点A北偏西30°方向，距观测点A直线距离600米．由于观测点A和目标点B之间被一片湿地分隔，无法直接通行，小明根据地形决定从观测点A出发，沿东北方向走一段距离后，到达位于目标点B南偏东75°方向的C处，求小明还要走多远才能到达目标点B？（结果保留根号）