题目内容
12.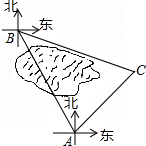 五一期间,小明同学到滨湖湿地公园参加校无线电测向科技社团组织的实践活动,目标点B在观测点A北偏西30°方向,距观测点A直线距离600米.由于观测点A和目标点B之间被一片湿地分隔,无法直接通行,小明根据地形决定从观测点A出发,沿东北方向走一段距离后,到达位于目标点B南偏东75°方向的C处,求小明还要走多远才能到达目标点B?(结果保留根号)
五一期间,小明同学到滨湖湿地公园参加校无线电测向科技社团组织的实践活动,目标点B在观测点A北偏西30°方向,距观测点A直线距离600米.由于观测点A和目标点B之间被一片湿地分隔,无法直接通行,小明根据地形决定从观测点A出发,沿东北方向走一段距离后,到达位于目标点B南偏东75°方向的C处,求小明还要走多远才能到达目标点B?(结果保留根号)
分析 作AD⊥BC于D,根据方向角可知∠ABD=45°,根据勾股定理求出BD的长,根据题意求出∠C=60°,根据正切的概念求出CD的长,求和即可.
解答 解:作AD⊥BC于D,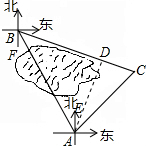
∵∠EAB=30°,AE∥BF,
∴∠FBA=30°,又∠FBC=75°,
∴∠ABD=45°,又AB=600米,
∴AD=DB=300$\sqrt{2}$米,
∵∠BAC=∠BAE+∠CAE=75°,∠ABC=45°,
∴∠C=60°,
tan∠C=$\frac{AD}{CD}$,
∴CD=$\frac{AD}{tan∠C}$=100$\sqrt{6}$,
∴BC=BD+CD=300$\sqrt{2}$+100$\sqrt{6}$(米).
答:小明还要走(300$\sqrt{2}$+100$\sqrt{6}$)米才能到达目标点B.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、熟记锐角三角函数的概念是解题的关键.

练习册系列答案
相关题目
17.据某网站统计,全国每年浪费食物总量约为50100000000千克,将50100000000用科学记数法表示为( )
| A. | 5.01×1010 | B. | 5.01×109 | C. | 50.1×109 | D. | 0.501×1010 |
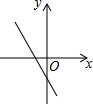
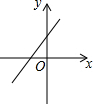
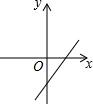
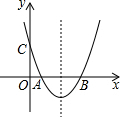 如图,关于x的二次函数y=x2-x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a-1)x+m的图象可能是( )
如图,关于x的二次函数y=x2-x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a-1)x+m的图象可能是( )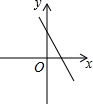
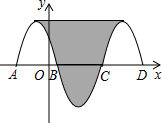 如图,抛物线y=-x2-2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为32.
如图,抛物线y=-x2-2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为32.
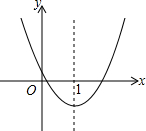 如图,二次函数y=ax2+bx+c的图象如图所示,则下列说法①ac<0;②2a+b<0;③当x=1时,a+b+c>0;④当x=-1时,a-b+c>0;⑤关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根.你认为其中正确的有( )
如图,二次函数y=ax2+bx+c的图象如图所示,则下列说法①ac<0;②2a+b<0;③当x=1时,a+b+c>0;④当x=-1时,a-b+c>0;⑤关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根.你认为其中正确的有( )