题目内容
2.观察图填空:已知正方形的边长为a,则:
(1)图①中阴影部分的面积是$\frac{4-π}{4}$a2;
(2)图②中阴影部分的面积是$\frac{4-π}{4}$a2;
(3)图③中阴影部分的面积是$\frac{4-π}{4}$a2.
由此你发现了什么,能用一句话来描述你发现的规律吗?
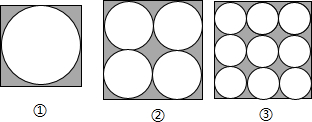
分析 (1)阴影部分的面积=正方形的面积-圆的面积;
(2)阴影部分的面积=正方形的面积-4个圆的面积;
(3)阴影部分的面积=正方形的面积-9个圆的面积;
它们的面积都相等.
解答 解:(1)S阴影=a2-π($\frac{1}{2}$a)2=$\frac{4-π}{4}$a2;
故答案是:$\frac{4-π}{4}$a2;
(2)S阴影=a2-4($\frac{1}{4}$π•$\frac{1}{4}$a2)=$\frac{4-π}{4}$a2;
故答案是:$\frac{4-π}{4}$a2;
(3)S阴影=a2-9($\frac{1}{4}$π•$\frac{1}{9}$a2)=$\frac{4-π}{4}$a2;
故答案是:$\frac{4-π}{4}$a2;
规律:所有的阴影部分的面积都相等.
点评 本题考查了列代数式.解题时,利用了“分割法”来求阴影部分的面积.

练习册系列答案
相关题目
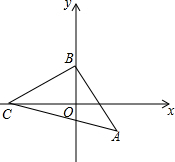 如图,已知B(0,1),C(-2,0),过点B作AB⊥BC,使得AB=BC.
如图,已知B(0,1),C(-2,0),过点B作AB⊥BC,使得AB=BC.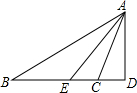 如图,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线,AD是BC边上的高,求∠DAE的大小.
如图,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线,AD是BC边上的高,求∠DAE的大小.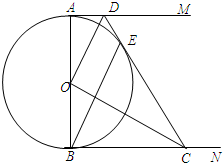 如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,
如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,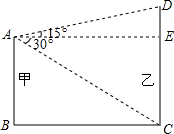 如图,平地上有甲乙两楼,甲楼高15米.已知从甲楼顶测得乙楼底的俯角为30°,又测得乙楼顶的仰角为15°.求乙楼的高.(tan15°=0.2679,精确到0.01)
如图,平地上有甲乙两楼,甲楼高15米.已知从甲楼顶测得乙楼底的俯角为30°,又测得乙楼顶的仰角为15°.求乙楼的高.(tan15°=0.2679,精确到0.01) 如图,⊙O直径AB与弦CD相交于E,∠AED=60°,AE=3,BE=7,求CD长.
如图,⊙O直径AB与弦CD相交于E,∠AED=60°,AE=3,BE=7,求CD长.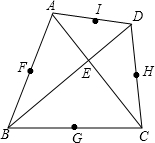 已知:如图,四边形ABCD的对角线AC⊥BD,垂足为E,点F,G,H,I分别是四边形各边中点.求证:F,G,H,I四个点在同一个圆上.
已知:如图,四边形ABCD的对角线AC⊥BD,垂足为E,点F,G,H,I分别是四边形各边中点.求证:F,G,H,I四个点在同一个圆上.