题目内容
17.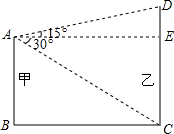 如图,平地上有甲乙两楼,甲楼高15米.已知从甲楼顶测得乙楼底的俯角为30°,又测得乙楼顶的仰角为15°.求乙楼的高.(tan15°=0.2679,精确到0.01)
如图,平地上有甲乙两楼,甲楼高15米.已知从甲楼顶测得乙楼底的俯角为30°,又测得乙楼顶的仰角为15°.求乙楼的高.(tan15°=0.2679,精确到0.01)
分析 在△ACE中,根据∠E=90°,∠CAE=30°,EC=15米,求出AC、AE的长度,然后在△ADE中求出DE的长度,继而可求出CD的高度.
解答 解:如图,在△ACE中,
∵∠E=90°,∠CAE=30°,EC=15米,
则AC=15×2=30(米),
AE=$\sqrt{3{0}^{2}-1{5}^{2}}$=15$\sqrt{3}$≈25.98(米),
又∵DE=AEtan15°=25.98×0.267=6.94(米),
∴乙楼DC=CE+ED=15+6.94=21.94(米).
答:乙楼的高约为21.94米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据所给的仰角和俯角构造直角三角形,利用三角函数的知识求解.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
12.对函数y=x+1与函数y=-$\frac{1}{x}$,下列表述中正确的是( )
| A. | 两个函数图象都经过第四象限 | |
| B. | 两个函数图象有两个公共点 | |
| C. | 两个函数在自变量的取值范围内y都随x的增大而增大 | |
| D. | 在第二象限内,函数y=x+1的值小于函数y=-$\frac{1}{x}$的值 |
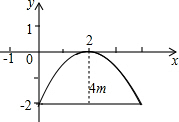 某次军事学习时,我军挖了一个横截面为抛物线的防空洞,尺寸如图.
某次军事学习时,我军挖了一个横截面为抛物线的防空洞,尺寸如图.