题目内容
14. 如图,⊙O直径AB与弦CD相交于E,∠AED=60°,AE=3,BE=7,求CD长.
如图,⊙O直径AB与弦CD相交于E,∠AED=60°,AE=3,BE=7,求CD长.
分析 过点O作OF⊥CD于点F,根据AE=3,BE=7求出OC的长,进而可得出OE的长,由∠AED=60°求出OF的长,根据勾股定理求出CF的长,由此可得出结论.
解答 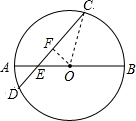 解:过点O作OF⊥CD于点F,
解:过点O作OF⊥CD于点F,
∵AE=3,BE=7,
∴OC=OA=5,
∴OE=5-3=2.
∵∠AED=60°,
∴∠OEF=60°,
∴OF=OE•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
在Rt△OCF中,
∵OC=5,OF=$\sqrt{3}$,
∴CF=$\sqrt{{OC}^{2}-{OF}^{2}}$=$\sqrt{{5}^{2}-{(\sqrt{3})}^{2}}$=$\sqrt{22}$,
∴CD=2CF=2$\sqrt{22}$.
点评 本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
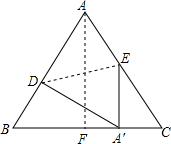 如图,△ABC是正三角形,点E是AC边上的中点,将三角形的一部分沿着DE折叠,使得点A于BC边上的某一点A′重合,若∠BEA′-∠A′EC=∠BAC,求∠ADE.
如图,△ABC是正三角形,点E是AC边上的中点,将三角形的一部分沿着DE折叠,使得点A于BC边上的某一点A′重合,若∠BEA′-∠A′EC=∠BAC,求∠ADE.
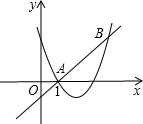 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B,且当x=4时,二次函数的值为6.
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B,且当x=4时,二次函数的值为6.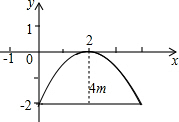 某次军事学习时,我军挖了一个横截面为抛物线的防空洞,尺寸如图.
某次军事学习时,我军挖了一个横截面为抛物线的防空洞,尺寸如图.