题目内容
13.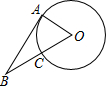 如图,已知AB为⊙O的切线,切点为A,连接BO,BO与⊙O交于点C,若AB=2CO,则sin∠ABO的值为( )
如图,已知AB为⊙O的切线,切点为A,连接BO,BO与⊙O交于点C,若AB=2CO,则sin∠ABO的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\sqrt{5}$ |
分析 由条件可求得AB=2AO,再由切线的性质可得△AOB为直角三角形,利用勾股定理可求得OB与AO的关系,由三角函数定义可求得答案.
解答 解:
∵AB=2CO,且AO=CO,
∴AB=2AO,
∵AB为⊙O的切线,
∴OA⊥AB,
∴△AOB为直角三角形,
∴BO=$\sqrt{A{O}^{2}+A{B}^{2}}$=$\sqrt{A{O}^{2}+4A{O}^{2}}$=$\sqrt{5}$AO,
∴sin∠ABO=$\frac{AO}{BO}$=$\frac{AO}{\sqrt{5}AO}$=$\frac{\sqrt{5}}{5}$,
故选C.
点评 本题主要考查切线的性质,证得△ABO为直角三角形,找到BO与AO的关系是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
4. 如图,扇形的半径为12,圆心角为60°,⊙O为扇形的内切圆,则阴影部分的面积等于( )
如图,扇形的半径为12,圆心角为60°,⊙O为扇形的内切圆,则阴影部分的面积等于( )
 如图,扇形的半径为12,圆心角为60°,⊙O为扇形的内切圆,则阴影部分的面积等于( )
如图,扇形的半径为12,圆心角为60°,⊙O为扇形的内切圆,则阴影部分的面积等于( )| A. | 8 | B. | 8π | C. | 20 | D. | 20π |
1.下列说法中,
①平分弦的直径垂直于弦;
②直径是最长的弦;
③两个三角形全等,那么它们关于一点成中心对称;
④长度相等的弧是等弧;
⑤x2-5x+7=0两根之和为5.
其中正确命题的个数为( )
①平分弦的直径垂直于弦;
②直径是最长的弦;
③两个三角形全等,那么它们关于一点成中心对称;
④长度相等的弧是等弧;
⑤x2-5x+7=0两根之和为5.
其中正确命题的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
8.若xm+3x-6=0是关于x的一元二次方程,则m的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.已知2a=3b,则$\frac{a}{b}$的值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
2.若关于x的不等式3x-a≤0的正整数解是1、2、3,则a应满足的条件是( )
| A. | a=9 | B. | a≤9 | C. | 9<a≤12 | D. | 9≤a<12 |
 已知,y=-$\frac{4}{3}$x+4与x轴,y轴的交点分别是点A,B,点C(-2,3),O是原点,求点C到直线AB的距离.
已知,y=-$\frac{4}{3}$x+4与x轴,y轴的交点分别是点A,B,点C(-2,3),O是原点,求点C到直线AB的距离. 四个三角形中,根据图中所标条件,能判断与左边的三角形全等的三角形是( )
四个三角形中,根据图中所标条件,能判断与左边的三角形全等的三角形是( )



 已知:如图,EF是△ABC的中位线,外角∠ACG的平分线交EF的延长线于点D,求证:AD⊥CD.
已知:如图,EF是△ABC的中位线,外角∠ACG的平分线交EF的延长线于点D,求证:AD⊥CD.