题目内容
5．已知2a=3b，则$\frac{a}{b}$的值为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{2}{5}$ | D． | $\frac{5}{2}$ |
分析 根据等式的性质，可得答案．
解答 解：两边都除以2b，得
$\frac{a}{b}$=$\frac{3}{2}$，
故选：B．
点评 本题考查了比例的性质，利用等式的性质是解题关键．
练习册系列答案
相关题目
15．
如图，AB∥CD，CD⊥EF，若∠1=124°，则∠2=（ ）
如图，AB∥CD，CD⊥EF，若∠1=124°，则∠2=（ ）| A． | 56° | B． | 66° | C． | 24° | D． | 34° |
16．下列调查中，调查方式选择不合理的是（ ）
| A． | 了解某电视台某次“爱的奉献”抗震救灾文艺晚会的收视率，采用抽样调查的方式 | |
| B． | 了解某渔场中青鱼的平均重量，采用抽样调查 | |
| C． | 了解某型号联想电脑的使用寿命，采用全面调查 | |
| D． | 了解一批汽车的刹车性能，采用全面调查 |
13．
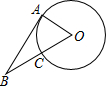如图，已知AB为⊙O的切线，切点为A，连接BO，BO与⊙O交于点C，若AB=2CO，则sin∠ABO的值为（ ）
如图，已知AB为⊙O的切线，切点为A，连接BO，BO与⊙O交于点C，若AB=2CO，则sin∠ABO的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{5}$ | C． | $\frac{\sqrt{5}}{5}$ | D． | $\sqrt{5}$ |
20．在函数y=$\frac{\sqrt{x+3}}{2x}$中，自变量x的取值范围是（ ）
| A． | x≥-3且x≠0 | B． | x≤3且x≠0 | C． | x≠0 | D． | x≥-3 |
10．若A（-1，y1），B（1，y2），C（2，y3）是y=$\frac{2}{x}$上的三个点，则y1，y2，y3之间的大小关系正确的是（ ）
| A． | y1＞y2＞y3 | B． | y1＜y2＜y3 | C． | y3＞y1＞y2 | D． | y1＜y3＜y2 |
17．若当x=3时，代数式x2+mx+2有最小值，则当x2+mx=7时，x的值为（ ）
| A． | x=0或x=6 | B． | x=1或x=7 | C． | x=1或x=-7 | D． | x=-1或x=7 |
14．4.9×105是一个由四舍五入得到的近似数，它是（ ）
| A． | 精确到百分位 | B． | 精确到十分位 | C． | 精确到万位 | D． | 精确到十万位 |
15．直角三角形的两条直角边长分别是3，4，则该直角三角形的斜边长是（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |