题目内容
3. 已知:如图,EF是△ABC的中位线,外角∠ACG的平分线交EF的延长线于点D,求证:AD⊥CD.
已知:如图,EF是△ABC的中位线,外角∠ACG的平分线交EF的延长线于点D,求证:AD⊥CD.
分析 根据角平分线的定义得到∠ACD=∠GCD,根据三角形中位线定理得到EF∥BC,AF=FC,得到DF=FC=FA,根据直角三角形的判定定理证明结论.
解答 证明:∵CD是外角∠ACG的平分线,
∴∠ACD=∠GCD,
∵EF是△ABC的中位线,
∴EF∥BC,AF=FC,
∴∠EDC=∠GCD,
∴∠ACD=∠EDC,
∴DF=FC,
∴DF=FC=FA,
∴∠ADC=90°,即AD⊥CD.
点评 本题考查的是三角形中位线定理、角平分线的定义、直角三角形的判定,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
13.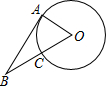 如图,已知AB为⊙O的切线,切点为A,连接BO,BO与⊙O交于点C,若AB=2CO,则sin∠ABO的值为( )
如图,已知AB为⊙O的切线,切点为A,连接BO,BO与⊙O交于点C,若AB=2CO,则sin∠ABO的值为( )
 如图,已知AB为⊙O的切线,切点为A,连接BO,BO与⊙O交于点C,若AB=2CO,则sin∠ABO的值为( )
如图,已知AB为⊙O的切线,切点为A,连接BO,BO与⊙O交于点C,若AB=2CO,则sin∠ABO的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\sqrt{5}$ |
14.4.9×105是一个由四舍五入得到的近似数,它是( )
| A. | 精确到百分位 | B. | 精确到十分位 | C. | 精确到万位 | D. | 精确到十万位 |
11.一元二次方程x2+2x-1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
8. 如图所示,AD平分∠BAC,AB=AC,连结BD、CD并延长分别交AC、AB于F、E点,则此图中全等三角形的对数为( )
如图所示,AD平分∠BAC,AB=AC,连结BD、CD并延长分别交AC、AB于F、E点,则此图中全等三角形的对数为( )
 如图所示,AD平分∠BAC,AB=AC,连结BD、CD并延长分别交AC、AB于F、E点,则此图中全等三角形的对数为( )
如图所示,AD平分∠BAC,AB=AC,连结BD、CD并延长分别交AC、AB于F、E点,则此图中全等三角形的对数为( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
15.直角三角形的两条直角边长分别是3,4,则该直角三角形的斜边长是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
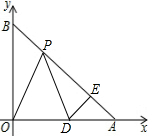 已知在平面直角坐标系中,A(a,0)、B(0,b)满足$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
已知在平面直角坐标系中,A(a,0)、B(0,b)满足$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E. 如图所示,长方形OABC的顶点A在x轴上,C在y轴上,点B坐标为(4,2),若直线y=mx-1恰好将长方形分成面积相等的两部分,则m的值为1.
如图所示,长方形OABC的顶点A在x轴上,C在y轴上,点B坐标为(4,2),若直线y=mx-1恰好将长方形分成面积相等的两部分,则m的值为1.