题目内容
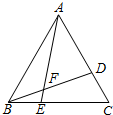已知△ABC是等边三角形，点D、E分别在AC、BC上，且CD=BE，则∠AFB=考点：全等三角形的判定与性质,等边三角形的性质
专题：
分析：根据等边三角形的性质可得AB=BC，∠ABC=∠C=60°，然后利用“边角边”证明△ABE和△BCD全等，根据全等三角形对应角相等可得∠BAE=∠CBD，从而求出∠BAE+∠ABF=∠ABC=60°，再根据三角形的内角和等于180°列式计算即可得解．
解答：解：∵△ABC是等边三角形，
∴AB=BC，∠ABC=∠C=60°，
在△ABE和△BCD中，
，
∴△ABE≌△BCD（SAS），
∴∠BAE=∠CBD，
∴∠BAE+∠ABF=∠CBD+∠ABF=∠ABC=60°，
在△ABF中，∠AFB=180°-（∠BAE+∠ABF）=180°-60°=120°．
故答案为：120．
∴AB=BC，∠ABC=∠C=60°，
在△ABE和△BCD中，
|
∴△ABE≌△BCD（SAS），
∴∠BAE=∠CBD，
∴∠BAE+∠ABF=∠CBD+∠ABF=∠ABC=60°，
在△ABF中，∠AFB=180°-（∠BAE+∠ABF）=180°-60°=120°．
故答案为：120．
点评：本题考查了全等三角形的判定与性质，等边三角形的性质，熟记性质并确定出全等三角形以及三角形全等的条件是解题的关键．
练习册系列答案
天天练口算系列答案
相关题目
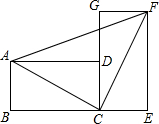把两个全等的矩形ABCD和矩形CEFG拼成如图所示的图案，若BC=4，AB=2，则△ACF的面积为
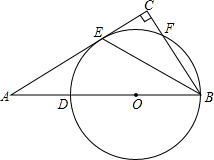如图，Rt△ABC中，∠C=90°，D在AB上，BE平分∠ABC交AC于点E，以BD为直径的圆经过点E，交BC于点F．
如图，AB⊥BD，ED⊥BD，C是BD上的一点，BC=DE，AB=CD．求证：AC⊥CE．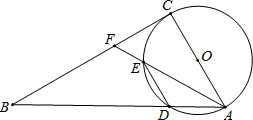
如图，以Rt△ABC的边AC为直径的⊙O交斜边AB于点D，点F为BC上一点，AF交⊙O于点E，且DE∥AC．
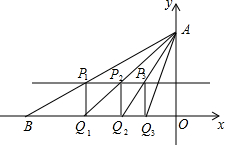已知直角坐标系中，点A（0，3），B（-6，0）．连结AB，作直线y=1，交AB于点P1，过P1作P1Q1⊥x轴于Q1；连结AQ1，交直线y=1于点P2，P2Q2⊥x轴于Q2；…以此类推．则点Q3的坐标为