题目内容
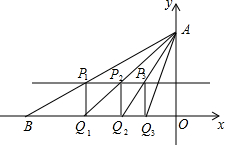 已知直角坐标系中,点A(0,3),B(-6,0).连结AB,作直线y=1,交AB于点P1,过P1作P1Q1⊥x轴于Q1;连结AQ1,交直线y=1于点P2,P2Q2⊥x轴于Q2;…以此类推.则点Q3的坐标为
已知直角坐标系中,点A(0,3),B(-6,0).连结AB,作直线y=1,交AB于点P1,过P1作P1Q1⊥x轴于Q1;连结AQ1,交直线y=1于点P2,P2Q2⊥x轴于Q2;…以此类推.则点Q3的坐标为考点:相似三角形的判定与性质,坐标与图形性质
专题:规律型
分析:①由P1Q1⊥x轴于Q1,P2Q2⊥x轴于Q2,…,以此类推.可得:P1Q1∥P2Q2∥P3Q3∥…∥PnQn∥y轴,进而可得△BP1Q1∽△ABO,△P2Q1Q2∽△AQ1O,△P3Q2Q3∽△AQ2O,…,然后根据相似三角形的对应边成比例,可求出BQ1,Q1Q2,Q2Q3,…的值,进而可确定Q1,Q2,Q3的坐标及P1,P2,P3的坐标,然后根据Q1,Q2,Q3的坐标及P1,P2,P3的坐标,寻求规律,归纳出Pn,Qn的坐标;
②根据△AP1Q1的面积=△ABQ1的面积-△BP1Q1的面积=
•BQ1•OA-
•BQ1•P1Q1=BQ1,△AP2Q2的面积=△AQ1Q2的面积-△Q1P 2Q2的面积=
•Q1Q2•OA-
•Q1Q2•P2Q2=Q1Q2,…,可得归纳出:△PnQnA的面积=Qn-1Qn,然后将Qn-1,Qn的横坐标代入即可.
②根据△AP1Q1的面积=△ABQ1的面积-△BP1Q1的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:①∵点A(0,3),B(-6,0),作直线y=1,交AB于点P1,
∴OA=3,OB=6,P1Q1=P2Q2=P3Q3=1,
∵P1Q1⊥x轴于Q1,P2Q2⊥x轴于Q2,…,
∴P1Q1∥P2Q2∥P3Q3∥…∥PnQn∥y轴,
∴△BP1Q1∽△ABO,△P2Q1Q2∽△AQ1O,△P3Q2Q3∽△AQ2O,…,
∴
=
,
=
,
=
,…,
∴BQ1=2,Q1Q2=
,Q2Q3=
,…,
∴Q1(-4,0),Q2(-
,0),Q3(-
,0),…,
P1(-4,1),P2(-
,1),P3(-
,0),…,
即Q1(-
,0),Q2(-
,0),Q3(-
,0),…,
P1(-
,1),P2(-
,1),P3(-
,0),…,
∴Qn-1(-
,0),Qn(-
,0),Pn-1(-
,1)Pn(-
,1),
故点Q3的坐标为:Q3(-
,0),
故答案为:Q3(-
,0);
②∵△AP1Q1的面积=△ABQ1的面积-△BP1Q1的面积=
•BQ1•OA-
•BQ1•P1Q1=BQ1,
△AP2Q2的面积=△AQ1Q2的面积-△Q1P 2Q2的面积=
•Q1Q2•OA-
•Q1Q2•P2Q2=Q1Q2,…,
∴△PnQnA的面积=Qn-1Qn=
-
=-
.
故答案为:-
.
∴OA=3,OB=6,P1Q1=P2Q2=P3Q3=1,
∵P1Q1⊥x轴于Q1,P2Q2⊥x轴于Q2,…,
∴P1Q1∥P2Q2∥P3Q3∥…∥PnQn∥y轴,
∴△BP1Q1∽△ABO,△P2Q1Q2∽△AQ1O,△P3Q2Q3∽△AQ2O,…,
∴
| P1Q1 |
| OA |
| BQ1 |
| OB |
| P2Q2 |
| OA |
| Q1Q2 |
| OQ1 |
| P3Q3 |
| OA |
| Q2Q3 |
| OQ2 |
∴BQ1=2,Q1Q2=
| 4 |
| 3 |
| 8 |
| 9 |
∴Q1(-4,0),Q2(-
| 8 |
| 3 |
| 16 |
| 9 |
P1(-4,1),P2(-
| 8 |
| 3 |
| 16 |
| 9 |
即Q1(-
| 22 |
| 30 |
| 23 |
| 31 |
| 24 |
| 32 |
P1(-
| 22 |
| 30 |
| 23 |
| 31 |
| 24 |
| 32 |
∴Qn-1(-
| 2n |
| 3n-2 |
| 2n+1 |
| 3n-1 |
| 2n |
| 3n-2 |
| 2n+1 |
| 3n-1 |
故点Q3的坐标为:Q3(-
| 16 |
| 9 |
故答案为:Q3(-
| 16 |
| 9 |
②∵△AP1Q1的面积=△ABQ1的面积-△BP1Q1的面积=
| 1 |
| 2 |
| 1 |
| 2 |
△AP2Q2的面积=△AQ1Q2的面积-△Q1P 2Q2的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴△PnQnA的面积=Qn-1Qn=
| 2n+1 |
| 3n-1 |
| 2n |
| 3n-2 |
| 2n |
| 3n-1 |
故答案为:-
| 2n |
| 3n-1 |
点评:此题考查了相似三角形的判断与性质及三角形的面积公式,解题的关键是:根据Q1,Q2,Q3的坐标及P1,P2,P3的坐标,寻求规律,归纳出Pn,Qn的坐标.

练习册系列答案
相关题目
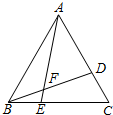 已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFB=
已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFB= 如图,已知D、E分别是△ABC中AB、AC边上的点,DE∥BC且
如图,已知D、E分别是△ABC中AB、AC边上的点,DE∥BC且
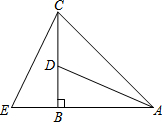 如图,在△ABC中,∠ABC=90°,AB=BC,点D在边BC上,点E在AB的延长线上,且BE=BD.
如图,在△ABC中,∠ABC=90°,AB=BC,点D在边BC上,点E在AB的延长线上,且BE=BD. 关于x的方程x2-
关于x的方程x2-