题目内容
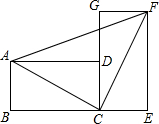 把两个全等的矩形ABCD和矩形CEFG拼成如图所示的图案,若BC=4,AB=2,则△ACF的面积为
把两个全等的矩形ABCD和矩形CEFG拼成如图所示的图案,若BC=4,AB=2,则△ACF的面积为考点:等腰直角三角形,勾股定理
专题:
分析:根据四边形ABCD,EFGC为全等的矩形,得到AB=CE,∠B=∠E=90°,BC=EF,即可得到△ABC≌△CEF,根据全等的性质得到∠ACB=∠CFE,AC=CF,再根据角角之间的关系得到∠ACF=90°,于是判断出△ACF的形状,进而根据三角形的面积公式即可求得.
解答:解:在RT△ABC中,AC=
=
=
,
∵四边形ABCD,EFGC为全等的矩形,
∴AB=CE,∠B=∠E=90°,BC=EF,
在△ABC和△CEF中,
,
∴△ABC≌△CEF(SAS),
∴∠ACB=∠CFE,AC=CF,
∵点B、C、E共线,
∴∠ABC+∠ACF+∠FCE=180°,
∴∠ACF=180°-(∠ECF+∠EFC)=90°,
∴△ACF是等腰直角三角形,
∴AC=CF=
,
∴S△ACF=
AC•CF=10.
故答案为10.
| AB2+BC2 |
| 22+42 |
| 20 |
∵四边形ABCD,EFGC为全等的矩形,
∴AB=CE,∠B=∠E=90°,BC=EF,
在△ABC和△CEF中,
|
∴△ABC≌△CEF(SAS),
∴∠ACB=∠CFE,AC=CF,
∵点B、C、E共线,
∴∠ABC+∠ACF+∠FCE=180°,
∴∠ACF=180°-(∠ECF+∠EFC)=90°,
∴△ACF是等腰直角三角形,
∴AC=CF=
| 20 |
∴S△ACF=
| 1 |
| 2 |
故答案为10.
点评:本题主要考查矩形的性质以及等腰直角三角形的判定,解答本题的关键是熟练掌握全等三角形的判定,此题难度不大.

练习册系列答案
相关题目
已知方程组
的解是
,则m、n之间的数量关系是( )
|
|
| A、m-16n=5 |
| B、m-16n=11 |
| C、m+16n=-11 |
| D、m+16n=-5 |
若双曲线y=
与直线y=2x+1的一个交点的横坐标为-1,则k的值为( )
| k |
| x |
| A、-1 | B、1 | C、-2 | D、2 |
 如图所示,AB是半圆O的直径,OC⊥AB,交
如图所示,AB是半圆O的直径,OC⊥AB,交
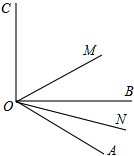 如图,已知∠AOC与∠AOB的和为180度,OM,ON分别是∠AOC、∠AOB的平分线.
如图,已知∠AOC与∠AOB的和为180度,OM,ON分别是∠AOC、∠AOB的平分线.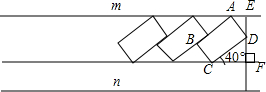 某住宅小区的物业管理部门为解决部门为解决住户停车困难问题,将一条道路开辟为停车场,停车位置如图所示,已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4m,BC=2.2m,∠DCF=40°.请计算停车位所占道路的宽度EF.(结果精确到0.1m)参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.
某住宅小区的物业管理部门为解决部门为解决住户停车困难问题,将一条道路开辟为停车场,停车位置如图所示,已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4m,BC=2.2m,∠DCF=40°.请计算停车位所占道路的宽度EF.(结果精确到0.1m)参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.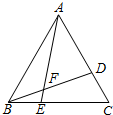 已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFB=
已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFB=